题目内容
6.若复数z=$\frac{i}{-1+2i}$,则$\overline{z}$的虚部为( )| A. | -$\frac{1}{5}$i | B. | -$\frac{1}{5}$ | C. | $\frac{1}{5}$i | D. | $\frac{1}{5}$ |
分析 直接利用复数代数形式的乘除运算化简,求出$\overline{z}$得答案.
解答 解:z=$\frac{i}{-1+2i}$=$\frac{i(-1-2i)}{(-1+2i)(-1-2i)}=\frac{2-i}{5}=\frac{2}{5}-\frac{i}{5}$,
∴$\overline{z}=\frac{2}{5}+\frac{i}{5}$.
∴$\overline{z}$的虚部为$\frac{1}{5}$.
故选:D.
点评 本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础的计算题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度y(米)随着时间t(0≤t≤24,单位:小时)而周期性变化.每天各时刻t的浪高数据的平均值如下表:
(1)试在图中描出所给点;
(2)观察图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定在一天内的7时至19时之间,当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.4 | 1.0 |
(2)观察图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定在一天内的7时至19时之间,当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
17.2015年8月12日天津发生危化品重大爆炸事故,造成重大人员和经济损失.某港口组织消防人员对该港口的公司的集装箱进行安全抽检,已知消防安全等级共分为四个等级(一级为优,二级为良,三级为中等,四级为差),该港口消防安全等级的统计结果如下表所示:
现从该港口随机抽取了n家公司,其中消防安全等级为三级的恰有20家.
(1)求m,n的值;
(2)按消防安全等级利用分层抽样的方法从这n家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
| 等 级 | 一级 | 二级 | 三级 | 四级 |
| 频 率 | 0.30 | 2m | m | 0.10 |
(1)求m,n的值;
(2)按消防安全等级利用分层抽样的方法从这n家公司中抽取10家,除去消防安全等级为一级和四级的公司后,再从剩余公司中任意抽取2家,求抽取的这2家公司的消防安全等级都是二级的概率.
1.已知函数f(x)=loga(x-m)的图象过点(4,0)和(7,1),则f(x)在定义域上是( )
| A. | 增函数 | B. | 减函数 | C. | 奇函数 | D. | 偶函数 |
18.设函数g(x)=x(x2-1),则g(x)在区间[0,1]上的最小值为( )
| A. | -1 | B. | 0 | C. | -$\frac{2\sqrt{3}}{9}$ | D. | $\frac{\sqrt{3}}{3}$ |
16.下列幂函数中,定义域是R且又是奇函数的是( )
| A. | $y={x^{\frac{3}{2}}}$ | B. | $y={x^{\frac{2}{3}}}$ | C. | $y={x^{-\frac{1}{3}}}$ | D. | $y={x^{\frac{1}{3}}}$ |
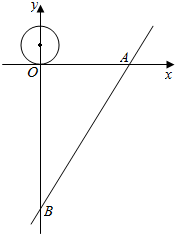 如图,在平面直角坐标系中,直线AB交x、y轴于点A(10$\sqrt{3}$,0),B(0,-30),一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒.
如图,在平面直角坐标系中,直线AB交x、y轴于点A(10$\sqrt{3}$,0),B(0,-30),一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒.