题目内容
4. 一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2016分钟结束之时,质点的位置坐标是(44,8).
一质点的移动方式,如图所示,在第1分钟,它从原点移动到点(1,0),接下来它便依图上所示的方向,在x,y轴的正向前进或后退,每1分钟只走1单位且平行其中一轴,则2016分钟结束之时,质点的位置坐标是(44,8).
分析 归纳走到(n,n)处时,移动的长度单位及方向.根据规律猜测出答案
解答 解:质点到达(1,1)处,走过的长度单位是2,方向向左;
质点到达(2,2)处,走过的长度单位是6=2+4,方向向下;
质点到达(3,3)处,走过的长度单位是12=2+4+6,方向向左;
质点到达(4,4)处,走过的长度单位是20=2+4+6+8,方向向下;
…
猜想:质点到达(n,n)处,走过的长度单位是2+4+6+…+2n=n(n+1),
且n为偶数时运动方向与y轴正半轴方向相反,n为奇数时运动方向与x轴正半轴方向相反.
所以2013分钟后是指质点到达(44,44)后,继续前进了33个单位,
由图中规律可得向下前进了23个单位,即质点位置是(44,8)
故答案为:44,8.
点评 本题考查了学生的阅读理解能力、归纳推理能力,解决本题的关键是读懂题意,并总结出一定的规律,这是高考的常考点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.某“帆板”集训队在一海滨区域进行集训,该海滨区域的海浪高度y(米)随着时间t(0≤t≤24,单位:小时)而周期性变化.每天各时刻t的浪高数据的平均值如下表:
(1)试在图中描出所给点;
(2)观察图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定在一天内的7时至19时之间,当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
| t(时) | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 |
| y(米) | 1.0 | 1.4 | 1.0 | 0.6 | 1.0 | 1.4 | 0.9 | 0.4 | 1.0 |
(2)观察图,从y=at+b,y=Asin(ωt+φ)+b,y=Acos(ωt+φ)中选择一个合适的函数模型,并求出该拟合模型的解析式;
(3)如果确定在一天内的7时至19时之间,当浪高不低于0.8米时才进行训练,试安排恰当的训练时间.
13.设全集U=R,集合A={x|log2x≤2},$B=\left\{{x|\frac{4}{3-x}≥1}\right\}$,则A∩B=( )
| A. | [-1,3) | B. | (-∞,-1]∪(3,4] | C. | (0,3] | D. | (0,3) |
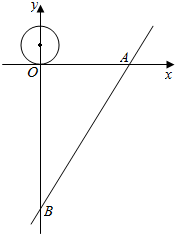 如图,在平面直角坐标系中,直线AB交x、y轴于点A(10$\sqrt{3}$,0),B(0,-30),一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒.
如图,在平面直角坐标系中,直线AB交x、y轴于点A(10$\sqrt{3}$,0),B(0,-30),一圆心位于(0,3),半径为3的动圆沿x轴向右滚动,动圆每6秒滚动一圈,则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒.