题目内容
2．求值：（1）若tanα=2，求$\frac{si{n}^{2}α+3sinα•cosα}{co{s}^{2}α-si{n}^{2}α}$；
（2）$\frac{1}{sin10°}$-$\frac{\sqrt{3}}{cos10°}$．
分析 （1）由条件利用同角三角函数的基本关系，求得要求式子的值．
（2）由条件利用两角和差的三角公式，二倍角公式，求得要求式子的值．
解答 （1）（1）若tanα=2，则 $\frac{si{n}^{2}α+3sinα•cosα}{co{s}^{2}α-si{n}^{2}α}$=$\frac{{tan}^{2}α+3tanα}{1{-tan}^{2}α}$=$\frac{4+3×2}{1-4}$=-$\frac{10}{3}$．
（2）$\frac{1}{sin10°}$-$\frac{\sqrt{3}}{cos10°}$=$\frac{cos10°-\sqrt{3}sin10°}{sin10°cos10°}$=$\frac{2sin（30°-10°）}{\frac{1}{2}sin20°}$=4．
点评 本题主要考查同角三角函数的基本关系，两角和差的三角公式，二倍角公式的应用，属于基础题．
练习册系列答案
相关题目
13．设全集U=R，集合A={x|log2x≤2}，$B=\left\{{x|\frac{4}{3-x}≥1}\right\}$，则A∩B=（ ）
| A． | [-1，3） | B． | （-∞，-1]∪（3，4] | C． | （0，3] | D． | （0，3） |
10．已知数列{cn}的前n项和为Tn，若数列{cn}满足各项均为正项，并且以（cn，Tn）（n∈N*）为坐标的点都在曲线$ay=\frac{a}{2}{x^2}+\frac{a}{2}x+b，（a为非0常数）$上运动，则称数列{cn}为“抛物数列”．已知数列{bn}为“抛物数列”，则（ ）
| A． | {bn}一定为等比数列 | B． | {bn}一定为等差数列 | ||
| C． | {bn}只从第二项起为等比数列 | D． | {bn}只从第二项起为等差数列 |
17．2015年8月12日天津发生危化品重大爆炸事故，造成重大人员和经济损失．某港口组织消防人员对该港口的公司的集装箱进行安全抽检，已知消防安全等级共分为四个等级（一级为优，二级为良，三级为中等，四级为差），该港口消防安全等级的统计结果如下表所示：
现从该港口随机抽取了n家公司，其中消防安全等级为三级的恰有20家．
（1）求m，n的值；
（2）按消防安全等级利用分层抽样的方法从这n家公司中抽取10家，除去消防安全等级为一级和四级的公司后，再从剩余公司中任意抽取2家，求抽取的这2家公司的消防安全等级都是二级的概率．
| 等 级 | 一级 | 二级 | 三级 | 四级 |
| 频 率 | 0.30 | 2m | m | 0.10 |
（1）求m，n的值；
（2）按消防安全等级利用分层抽样的方法从这n家公司中抽取10家，除去消防安全等级为一级和四级的公司后，再从剩余公司中任意抽取2家，求抽取的这2家公司的消防安全等级都是二级的概率．
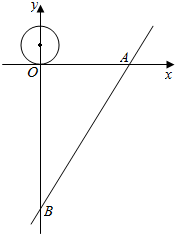如图，在平面直角坐标系中，直线AB交x、y轴于点A（10$\sqrt{3}$，0），B（0，-30），一圆心位于（0，3），半径为3的动圆沿x轴向右滚动，动圆每6秒滚动一圈，则动圆与直线AB第一次相切时所用的时间为$\frac{9\sqrt{3}}{π}$ 秒．