题目内容
18.已知圆C方程为:x2+y2=4.(1)直线l过点P(1,2),且与圆C交于A、B两点,若$|AB|=2\sqrt{3}$,求直线l的方程;
(2)过点P(1,2)作圆C的切线,设切点分别为M,N,求直线NM方程.
分析 (1)分直线l垂直于x轴时和直线l不垂直于x轴两种情况,分别求出满足$|AB|=2\sqrt{3}$的直线方程,综合可得得答案;
(2)设切点M(x1,y1),N(x2,y2),则可得切线PM和PN的方程,进而可得直线NM方程.
解答 解:(1)①当直线l垂直于x轴时,则此时直线方程为x=1,l与圆的两个交点坐标为$(1,\sqrt{3})$和$(1,-\sqrt{3})$,其距离为$2\sqrt{3}$满足题意;
②若直线l不垂直于x轴,设其方程为y-2=k(x-1),即kx-y-k+2=0,
设圆心到此直线的距离为d,则$2\sqrt{3}=2\sqrt{4-{d^2}}$,得d=1,
∴$1=\frac{|-k+2|}{{\sqrt{{k^2}+1}}}$,$k=\frac{3}{4}$,故所求直线方程为3x-4y+5=0,
综上所述,所求直线为3x-4y+5=0或x=1.
(2)设切点M(x1,y1),N(x2,y2),则切线PM方程为x1x+y1y=4,
切线PN方程为:x2x+y2y=4,
因为点P在直线QM上,则x1+2y1=4,
同理可得x2+2y2=4,
所以直线MN的方程为x+2y=4.
点评 本题考查的知识点是直线与圆的位置关系,弦长公式,直线方程,难度中档.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
9.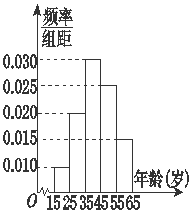 为了宣传在某市举行的“第十届中国艺术节”,筹委会举办了知识有奖问答活动,随机从15~65岁的市民中抽取n人,回答问题统计结果如图表所示:
为了宣传在某市举行的“第十届中国艺术节”,筹委会举办了知识有奖问答活动,随机从15~65岁的市民中抽取n人,回答问题统计结果如图表所示:
(1)求出a,x的值;
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,筹委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
 为了宣传在某市举行的“第十届中国艺术节”,筹委会举办了知识有奖问答活动,随机从15~65岁的市民中抽取n人,回答问题统计结果如图表所示:
为了宣传在某市举行的“第十届中国艺术节”,筹委会举办了知识有奖问答活动,随机从15~65岁的市民中抽取n人,回答问题统计结果如图表所示:| 组号 | 分组 | 回答正确 的人数 | 回答正确的人数 占本组的频率 |
| 第1组 | [15,25) | 5 | 0.5 |
| 第2组 | [25,35) | a | 0.9 |
| 第3组 | [35,45) | 27 | x |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65) | 3 | 0.2 |
(2)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,筹委会决定在所抽取的6人中随机抽取2人颁发幸运奖,求所抽取的人中第2组至少有1人获得幸运奖的概率.
10.若集合A={x|x2+3x-4>0},集合B={x|-1<x≤3},且M=A∩B,则有( )
| A. | -1∈M | B. | 0∈M | C. | 1∈M | D. | 2∈M |
17.已知,焦点在x轴上的椭圆的上、下顶点分别为B2、B1,左焦点和右顶点分别为F、A1.经过点B2的直线l与以椭圆的中心为顶点、B2为焦点的抛物线交于A、B两点,且点B2恰为线段AB的三等分点,直线l1过点B1且垂直于y轴,线段AB的中点M到直线l1的距离为$\frac{9}{4}$.若$\overrightarrow{F{B}_{2}}$•$\overrightarrow{{A}_{1}{B}_{2}}$=1-2$\sqrt{3}$,则椭圆的标准方程是( )
| A. | $\frac{{x}^{2}}{4}$+y2=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{3}$+y2=1 |
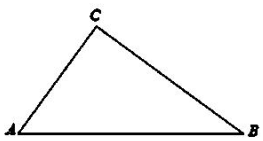 如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=10 千米,AC=6 千米,BC=8千米.现甲、乙两人同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为10千米/小时,乙的路线是ACB,速度为16千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.