题目内容
17.已知,焦点在x轴上的椭圆的上、下顶点分别为B2、B1,左焦点和右顶点分别为F、A1.经过点B2的直线l与以椭圆的中心为顶点、B2为焦点的抛物线交于A、B两点,且点B2恰为线段AB的三等分点,直线l1过点B1且垂直于y轴,线段AB的中点M到直线l1的距离为$\frac{9}{4}$.若$\overrightarrow{F{B}_{2}}$•$\overrightarrow{{A}_{1}{B}_{2}}$=1-2$\sqrt{3}$,则椭圆的标准方程是( )| A. | $\frac{{x}^{2}}{4}$+y2=1 | B. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{2}$=1 | C. | $\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{3}$+y2=1 |
分析 由抛物线的定义可知:丨AA′丨=丨AB2丨,丨BB′丨=丨BB2丨,丨AB丨=丨AB2丨+丨BB2丨,则丨AB丨=2丨MN丨=$\frac{9}{2}$,由点B2恰为线段AB的三等分点,根据相似三角形的性质即可求得丨B1B2丨=2,即2b=2,b=1,B2(0,1),F(-c,0),A1(a,0),由$\overrightarrow{F{B}_{2}}$•$\overrightarrow{{A}_{1}{B}_{2}}$=1-2$\sqrt{3}$,根据向量数量积的坐标运算,a2c2=12,由c2=a2-b2=a2-1,代入即可求得a的值,求得椭圆方程.
解答 解:设椭圆的标准方程:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由题意可知:线段AB的中点M到直线l1的距离为$\frac{9}{4}$,
由抛物线的定义可知:丨AA′丨=丨AB2丨,丨BB′丨=丨BB2丨,
∴丨AB丨=丨AB2丨+丨BB2丨,
∴丨AB丨=2丨MN丨=$\frac{9}{2}$,
由点B2恰为线段AB的三等分点,
∴丨AA′丨=丨AB2丨=$\frac{3}{2}$,丨BB′丨=丨BB2丨=3,
由相似三角形的性质可知:丨B1B2丨=2,即2b=2,b=1,
则B2(0,1),F(-c,0),A1(a,0),
$\overrightarrow{F{B}_{2}}$=(c,1),$\overrightarrow{{A}_{1}{B}_{2}}$=(-a,1),
$\overrightarrow{F{B}_{2}}$•$\overrightarrow{{A}_{1}{B}_{2}}$=-ac+1,
由$\overrightarrow{F{B}_{2}}$•$\overrightarrow{{A}_{1}{B}_{2}}$=1-2$\sqrt{3}$,则ac=2$\sqrt{3}$,a2c2=12,
由椭圆的性质可知:c2=a2-b2=a2-1,
代入可知:a2(a2-1)=12,整理得:a4-a2-12=0,
解得:a2=4,
∴椭圆的标准方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$,
故选A.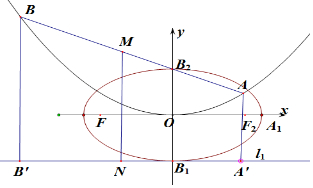
点评 本题考查椭圆的标准方程,考查椭圆及抛物线性质的简单应用,考查相似三角形的性质,考查计算能力,属于难题.

 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案| A. | 充分且不必要条件 | B. | 必要且不充分条件 | ||
| C. | 充要条件 | D. | 既非充分也非必要条件 |
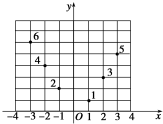 如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.
如图所示,坐标纸上的每个单元格的边长为1,由下往上的六个点:1,2,3,4,5,6的横、纵坐标分别对应数列{an}(n∈N*)的前12项,如表所示.| a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 |
| x1 | y1 | x2 | y2 | x3 | y3 | x4 | y4 | x5 | y5 | x6 | y6 |
| A. | 1 003 | B. | 1 005 | C. | 1 006 | D. | 2 010 |
| A. | 3,3 | B. | 4,3 | C. | 6,3 | D. | 8,3 |
| A. | -2 | B. | $-\frac{1}{2}$ | C. | 2 | D. | $\frac{1}{2}$ |
| A. | $\frac{1}{36}$ | B. | $\frac{1}{9}$ | C. | $\frac{1}{18}$ | D. | $\frac{1}{6}$ |