��Ŀ����
6��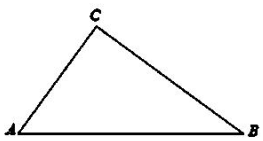 ��ͼ��A��B��C������ֱ����ͨ��AB=10 ǧ�ף�AC=6 ǧ�ף�BC=8ǧ�ף��ּס�������ͬʱ��A�س�������ǰ��B�أ�����tСʱ������֮��ľ���Ϊf��t������λ��ǧ�ף�����·����AB���ٶ�Ϊ10ǧ��/Сʱ���ҵ�·����ACB���ٶ�Ϊ16ǧ��/Сʱ���ҵ���B�غ�ԭ�صȴ�����t=t1ʱ�ҵ���C�أ�
��ͼ��A��B��C������ֱ����ͨ��AB=10 ǧ�ף�AC=6 ǧ�ף�BC=8ǧ�ף��ּס�������ͬʱ��A�س�������ǰ��B�أ�����tСʱ������֮��ľ���Ϊf��t������λ��ǧ�ף�����·����AB���ٶ�Ϊ10ǧ��/Сʱ���ҵ�·����ACB���ٶ�Ϊ16ǧ��/Сʱ���ҵ���B�غ�ԭ�صȴ�����t=t1ʱ�ҵ���C�أ���1����t1��f��t1�� ��ֵ��
��2����֪�Խ�������Чͨ��������3ǧ�ף���t1��t��1ʱ����f��t���ı���ʽ�����ж�f��t�� ��[t1��1]�ϵ����ֵ�Ƿ�3��˵�����ɣ�
���� ��1��������ɵ�t1=$\frac{3}{8}$h�������Ҷ����ɵ�f��t1��=CD=$\sqrt{A{C}^{2}+A{D}^{2}-2AC•ADcosA}$=$\frac{3\sqrt{41}}{4}$��
��2����t1=$\frac{3}{8}$��t��$\frac{7}{8}$ʱ������֪���ݺ����Ҷ����ɵ�f��t��=PQ=2$\sqrt{2{5t}^{2}-42t+18}$����$\frac{7}{8}$��t��1ʱ��f��t��=10-10t���ɵý��ۣ�
��� �⣺��1��������ɵ�t1=$\frac{3}{8}$h�����ҵ�Cʱ�����ڵ�ΪD����AD=$\frac{15}{4}$��ǧ�ף���
��������ACD�У������Ҷ���f��t1��=CD=$\sqrt{A{C}^{2}+A{D}^{2}-2AC•ADcosA}$=$\frac{3\sqrt{41}}{4}$��ǧ�ף���
��2������B��ʱ1Сʱ���ҵ���C��ʱ$\frac{3}{8}$Сʱ����A��B����ʱ$\frac{7}{8}$Сʱ��
��t1=$\frac{3}{8}$��t��$\frac{7}{8}$ʱ��
f��t��=$\sqrt{��14-16t��^{2}+��10-10t��^{2}-2��14-16t����10-10t��•\frac{4}{5}}$=2$\sqrt{2{5t}^{2}-42t+18}$��
��$\frac{7}{8}$��t��1ʱ��f��t��=10-10t��
��f��t��=$\left\{\begin{array}{l}{2\sqrt{25{t}^{2}-42t+18}��\frac{3}{8}��t��\frac{7}{8}}\\{10-10t��\frac{7}{8}��t��1}\end{array}\right.$��
��Ϊf��t����[$\frac{3}{8}$��$\frac{7}{8}$]�ϵ����ֵ��f��$\frac{3}{8}$��=$\frac{3\sqrt{41}}{4}$��f��t����[$\frac{7}{8}$��1]�ϵ����ֵ��f��$\frac{7}{8}$��=$\frac{5}{4}$��
����f��t����[$\frac{3}{8}$��1]�ϵ����ֵ��$\frac{3\sqrt{41}}{4}$������3��
���� ���⿼��������ε�ʵ��Ӧ�ã��漰���Ҷ����ͷֶκ��������е��⣮

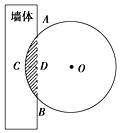 ���������������ҹ��Ŵ�������ѧ���䣮���жԹ��ɶ�����������������һǧ���꣬����������һ�����⣺������Բ�����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��ʾ����Σ�������Ϊ������һԲ����ľ�ģ�����ǽ���У���֪���С���þ�ȥ��ò��ϣ������һ�磬�����һ�ߣ������Բ����ľ�ϵ�ֱ���Ƕ��٣���Ϊ1�ɵ�Բ����ľ�IJ�����Ƕ��ǽ���У�����ͼ��ͼ��ʾ����Ӱ����Ϊ��Ƕ��ǽ���ڵIJ��֣�����֪��AB=1�ߣ����θ�CD=1�磬�����ľ����Ƕ��ǽ�е����ԼΪ�������� ��ע��1��=10��=100�磬�С�3.14��sin22.5���$\frac{5}{13}$��
���������������ҹ��Ŵ�������ѧ���䣮���жԹ��ɶ�����������������һǧ���꣬����������һ�����⣺������Բ�����ڱ��У���֪��С���Ծ��֮����һ�磬�����һ�ߣ��ʾ����Σ�������Ϊ������һԲ����ľ�ģ�����ǽ���У���֪���С���þ�ȥ��ò��ϣ������һ�磬�����һ�ߣ������Բ����ľ�ϵ�ֱ���Ƕ��٣���Ϊ1�ɵ�Բ����ľ�IJ�����Ƕ��ǽ���У�����ͼ��ͼ��ʾ����Ӱ����Ϊ��Ƕ��ǽ���ڵIJ��֣�����֪��AB=1�ߣ����θ�CD=1�磬�����ľ����Ƕ��ǽ�е����ԼΪ�������� ��ע��1��=10��=100�磬�С�3.14��sin22.5���$\frac{5}{13}$��| A�� | 600������ | B�� | 610������ | C�� | 620������ | D�� | 633������ |