题目内容
8.已知函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x<0}\\{{e}^{x},x≥0}\end{array}\right.$,则函数g(x)=f(x)-x-3的零点有2 个.分析 函数g(x)=f(x)-x-3的零点个数即函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x<0}\\{{e}^{x},x≥0}\end{array}\right.$的图象与函数y=x+3的图象的交点个数,数形结合,可得答案.
解答 解:函数f(x)=$\left\{\begin{array}{l}{{x}^{2}-x,x<0}\\{{e}^{x},x≥0}\end{array}\right.$的图象如下图所示: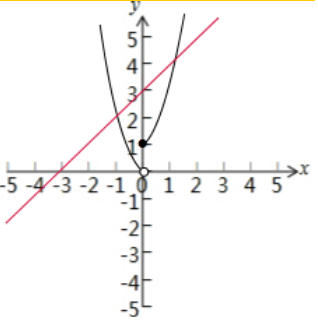
由图可得函数f(x)的图象与函数y=x+3的图象有2个交点,
故函数g(x)=f(x)-x-3有两个零点
故答案为:2.
点评 本题考查的知识点是函数的零点,分段函数的应用,函数的图象,难度中档.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
18.已知△ABC三边长成公差为2的等差数列,且最大角的正弦值为$\frac{{\sqrt{3}}}{2}$,则这个三角形的周长是( )
| A. | 13 | B. | 15 | C. | 18 | D. | 不确定 |
16.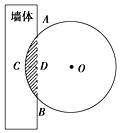 《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
 《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)
《九章算术》是我国古代著名数学经典.其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小.以锯锯之,深一寸,锯道长一尺.问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺.问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示(阴影部分为镶嵌在墙体内的部分).已知弦AB=1尺,弓形高CD=1寸,估算该木材镶嵌在墙中的体积约为( ) (注:1丈=10尺=100寸,π≈3.14,sin22.5°≈$\frac{5}{13}$)| A. | 600立方寸 | B. | 610立方寸 | C. | 620立方寸 | D. | 633立方寸 |
20.在△ABC中,角A,B,C所对边分别为a,b,c,若B=30°,b=2,c=2$\sqrt{3}$,则角C=( )
| A. | 60°或120° | B. | 60° | C. | 30°或150° | D. | 30° |
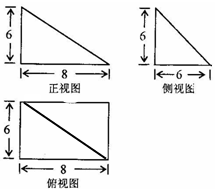 已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示).
已知某几何体的正视图、侧视图都是直角三角形,俯视图是矩形(尺寸如图所示).