题目内容
已知a，b，c∈R，给出下列命题：
①若a＞b，则ac2＞bc2；②若ab≠0，则
+
≥2；③若a＞|b|，则a2＞b2；
其中真命题的个数为（ ）
①若a＞b，则ac2＞bc2；②若ab≠0，则
| a |
| b |
| b |
| a |
其中真命题的个数为（ ）
| A、3 | B、2 | C、1 | D、0 |
考点：命题的真假判断与应用,不等式的基本性质
专题：不等式的解法及应用
分析：①当c=0时，不成立；
②当a与b异号时，
＜0，
＜0，不成立；
③由a＞|b|≥0，可得a2＞|b|2．
②当a与b异号时，
| a |
| b |
| b |
| a |
③由a＞|b|≥0，可得a2＞|b|2．
解答：
解：①当c=0时，ac2=bc2=0，∴①为假命题；
②当a与b异号时，
＜0，
＜0，∴②为假命题；
③∵a＞|b|≥0，∴a2＞|b|2，③为真命题．
综上可知：只有③是真命题．
故选：C．
②当a与b异号时，
| a |
| b |
| b |
| a |
③∵a＞|b|≥0，∴a2＞|b|2，③为真命题．
综上可知：只有③是真命题．
故选：C．
点评：本题考查了不等式的基本性质，属于基础题．
练习册系列答案
相关题目
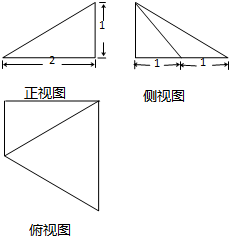某几何体的三视图如图所示，其中正（主）视图与侧（左）视图的边界均为直角三角形，俯视图的边界为直角梯形，则该几何体的体积是（ ）已知∠B是△ABC的一个内角，下列函数能取负值的是（ ）
| A、sinB | ||
| B、cosB | ||
C、tan
| ||
D、cos
|