题目内容
4．函数f（x）=lnx2-2的零点是（ ）| A． | e | B． | $\sqrt{e}$ | C． | -e | D． | e或-e |
分析 利用函数的零点与方程的解关系，直接化简求解即可．
解答 解：函数f（x）=lnx2-2的零点是方程：lnx2-2=0的解，
可得x2=e2，解得x=±e．
函数f（x）=lnx2-2的零点是：±e．
故选：D．
点评 本题考查函数的零点与方程根的关系，考查计算能力．
练习册系列答案
夺冠训练单元期末冲刺100分系列答案
新思维小冠军100分作业本系列答案
名师指导一卷通系列答案
相关题目
，且
，
，则
的取值范围是_______.
19．
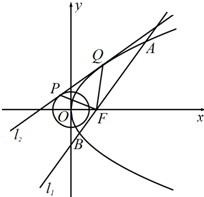如图，设抛物线C：y2=2px（p＞0）的焦点为F，过点F的直线l1交抛物线C于A，B两点，且|AB|=8，线段AB的中点到y轴的距离为3．直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P，与抛物线C切于点Q，则△FPQ的面积（ ）
如图，设抛物线C：y2=2px（p＞0）的焦点为F，过点F的直线l1交抛物线C于A，B两点，且|AB|=8，线段AB的中点到y轴的距离为3．直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P，与抛物线C切于点Q，则△FPQ的面积（ ）| A． | $\frac{3}{2}$ | B． | 2 | C． | $\frac{{\sqrt{3}}}{4}$ | D． | 1 |
16．
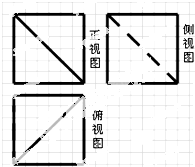如图，网格纸上小正方形的边长为1，粗线画出的是一正方体被截去一部分后所得几何体的三视图，则该几何体的表面积为（ ）
如图，网格纸上小正方形的边长为1，粗线画出的是一正方体被截去一部分后所得几何体的三视图，则该几何体的表面积为（ ）| A． | 54 | B． | 162 | C． | 54+18$\sqrt{3}$ | D． | 162+18$\sqrt{3}$ |
如图，在四棱锥P-ABCD中，底面ABCD是直角梯形，AB⊥AD，AB∥CD，$CD=2AB=2BP=\sqrt{2}AD$，$\overrightarrow{CE}=λ\overrightarrow{EB}$（λ＞0），DE⊥平面PBC，侧面ABP⊥底面ABCD