题目内容
7.设p,q为实数,$\overrightarrow{a},\overrightarrow{b}$是两个不共线向量,$\overrightarrow{AB}$=2$\overrightarrow{a}+p\overrightarrow{b}$,$\overrightarrow{BC}=\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{CD}=(q-1)\overrightarrow{a}-2\overrightarrow{b}$,若A,B,D三点共线,则pq的值是( )| A. | -1 | B. | 1 | C. | 2 | D. | -2 |
分析 要求三点共线问题,先求每两点对应的向量,然后再按两向量共线进行判断,本题知道$\overrightarrow{AB}$,要根据$\overrightarrow{BC}$和$\overrightarrow{CD}$算出$\overrightarrow{BD}$,再用向量共线的充要条件.
解答 解:因为$\overrightarrow{AB}$=2$\overrightarrow{a}+p\overrightarrow{b}$,$\overrightarrow{BC}=\overrightarrow{a}+\overrightarrow{b}$,$\overrightarrow{CD}=(q-1)\overrightarrow{a}-2\overrightarrow{b}$,
$\overrightarrow{BD}$=(2+q)$\overrightarrow{a}$+(p-1)$\overrightarrow{b}$,
又A,B,D三点共线,
∴$\overrightarrow{AB}=λ\overrightarrow{BD}$,
∴λ(2+q)=2,λ(p-1)=p,
化简得pq=-2,
故选D.
点评 本题考查三点共线问题,注意使用三点共线的充要条件,三点共线实质上就是两向量共线,容易出错的是向量共线的坐标形式.

练习册系列答案
相关题目
19.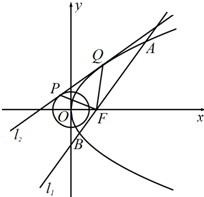 如图,设抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1交抛物线C于A,B两点,且|AB|=8,线段AB的中点到y轴的距离为3.直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P,与抛物线C切于点Q,则△FPQ的面积( )
如图,设抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1交抛物线C于A,B两点,且|AB|=8,线段AB的中点到y轴的距离为3.直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P,与抛物线C切于点Q,则△FPQ的面积( )
 如图,设抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1交抛物线C于A,B两点,且|AB|=8,线段AB的中点到y轴的距离为3.直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P,与抛物线C切于点Q,则△FPQ的面积( )
如图,设抛物线C:y2=2px(p>0)的焦点为F,过点F的直线l1交抛物线C于A,B两点,且|AB|=8,线段AB的中点到y轴的距离为3.直线l2与圆${x^2}+{y^2}=\frac{1}{2}$切于点P,与抛物线C切于点Q,则△FPQ的面积( )| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{{\sqrt{3}}}{4}$ | D. | 1 |
16.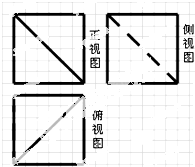 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )| A. | 54 | B. | 162 | C. | 54+18$\sqrt{3}$ | D. | 162+18$\sqrt{3}$ |
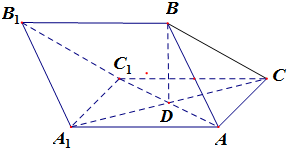 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D. ,且
,且 ,
, ,则
,则 的取值范围是_______.
的取值范围是_______.