题目内容
8. 根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.
根据最新修订的《环境空气质量标准》指出空气质量指数在0~50,各类人群可正常活动.某市环保局在2014年对该市进行了为期一年的空气质量检测,得到每天的空气质量指数,从中随机抽取50个作为样本进行分析报告,样本数据分组区间为[0,10),[10,20),[20,30),[30,40),[40,50],由此得到样本的空气质量指数频率分布直方图,如图.(Ⅰ)求a的值;并根据样本数据,试估计这一年度的空气
质量指数的平均值;
(Ⅱ)用这50个样本数据来估计全年的总体数据,将频率视为概率.如果空气质量指数不超过20,就认定空气质量为“最优等级”.从这一年的监测数据中随机抽取2天的数值,其中达到“最优等级”的天数为ξ,求ξ的分布列,并估计一个月(30天)中空气质量能达到“最优等级”的天数.
分析 (Ⅰ)由频率分布直方图能求出a的值和50个样本中空气质量指数的平均值,从而能估计2014年这一年度空气质量指数的平均值.
(Ⅱ)利用样本估计总体,该年度空气质量指数在[0,20]内为“最优等级”,且指数达到“最优等级”的概率为0.3,则ξ~B(2,0.3).由此能求出ξ的分布列和一个月(30天)中空气质量能达到“最优等级”的天数.
解答 解:(Ⅰ)由题意,得(0.03+0.032+a+0.01+0.008)×10=1,
解得a=0.02.…(3分)
50个样本中空气质量指数的平均值为:
$\overline X=0.1×5+0.2×15+0.32×25+0.3×35+0.08×45=25.6$
由样本估计总体,可估计2014年这一年度空气质量指数的平均值约为25.6 …(6分)
(Ⅱ)利用样本估计总体,该年度空气质量指数在[0,20]内为“最优等级”,
且指数达到“最优等级”的概率为0.3,则ξ~B(2,0.3).
ξ的可能取值为0,1,2,…(7分)
$P(ξ=0)=C_2^0{(0.3)^0}×{(0.7)^2}=\frac{49}{100},P(ξ=1)=C_2^1(0.3)×(0.7)=\frac{42}{100}$,
$P(ξ=2)=C_2^2{(0.3)^2}=\frac{9}{100}$…(10分)
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
| P | $\frac{49}{100}$ | $\frac{42}{100}$ | $\frac{9}{100}$ |
设一个月(30天)中空气质量能达到“最优等级”的天数为η,则η~B(30,0.3)
故一个月(30天)中空气质量能达到“最优等级”的天数大约为Eη=30×0.3=9天.…(13分)
点评 本题考查频率分直方图的应用,考查离散型随机变量的概率分布列的求法,在历年高考中都是必考题型之一.

练习册系列答案
相关题目
16.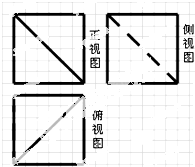 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )| A. | 54 | B. | 162 | C. | 54+18$\sqrt{3}$ | D. | 162+18$\sqrt{3}$ |
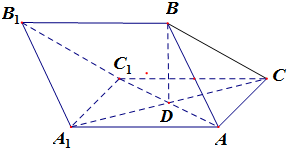 在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D.
在三棱柱ABC-A1B1C1中,AB=AC=AA1=BC1=2,∠AA1C1=60°,BC=$\sqrt{6}$,AC1与A1C相交于点D. ,且
,且 ,
, ,则
,则 的取值范围是_______.
的取值范围是_______.