题目内容
3.已知方程2x2+3x-1=0的一非零实根是x1,ax2+3x-1=0(a≠0)的一非零实根是x2.函数f(x)=$\frac{1}{3}{x^3}+\frac{3}{2}{x^2}$-x+3在(x1,x2)有且仅有一个极值点,则a的取值范围是[-$\frac{9}{4}$,0)∪(0,1].分析 由函数f(x)=$\frac{1}{3}{x^3}+\frac{3}{2}{x^2}$-x+3在(x1,x2)有且仅有一个极值点,得到f'(x)=x2+3x-1在(x1,x2)有且仅有一解,根据零点存在定理即可求出a的范围.
解答 解:∵2x2+3x-1=0的一非零实根是x1,ax2+3x-1=0(a≠0)的一非零实根是x2,
∵f(x)=$\frac{1}{3}{x^3}+\frac{3}{2}{x^2}$-x+3,
∴f'(x)=x2+3x-1,
∵函数f(x)=$\frac{1}{3}{x^3}+\frac{3}{2}{x^2}$-x+3在(x1,x2)有且仅有一个极值点
∴f'(x)=x2+3x-1在(x1,x2)有且仅有一解,
∴f′(x1)•f′(x2)=(x12+3x1-1)(x22+3x2-1)
=(2x12+3x1-1-x12)[ax22+3x2-1-(a-1)x22]=-(1-a)x12x22≤0,
∴1-a≥0,
∴a≤1,
又△=9+4a≥0,
∴$a≥-\frac{9}{4}$,
∴$-\frac{9}{4}≤a≤1$,
∵a≠0,
∴a的取值范围为[-$\frac{9}{4}$,0)∪(0,1],
故答案为:[-$\frac{9}{4}$,0)∪(0,1],
点评 本题考查了导数和函数的极值的关系以及函数零点存在定理,考查了学生的运算能力,属于中档题.

练习册系列答案
相关题目
16.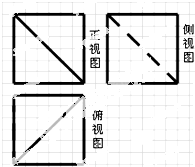 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
 如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )
如图,网格纸上小正方形的边长为1,粗线画出的是一正方体被截去一部分后所得几何体的三视图,则该几何体的表面积为( )| A. | 54 | B. | 162 | C. | 54+18$\sqrt{3}$ | D. | 162+18$\sqrt{3}$ |
18.某几何体的三视图如图所示,其中俯视图中半圆半径为$\sqrt{2}$,则该几何体的体积是( )
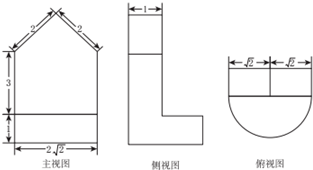

| A. | $2π+8\sqrt{2}+2$ | B. | $2π+8\sqrt{2}+1$ | C. | $π+8\sqrt{2}+1$ | D. | $π+8\sqrt{2}+2$ |
12.若f(x)=$\left\{{\begin{array}{l}{{a^x},x<0}\\{{{log}_a}x,x>0}\end{array}}$,那么y=f(x)-a的零点个数有( )
| A. | 0个 | B. | 1个 | ||
| C. | 2个 | D. | a的值不同时零点的个数不同 |
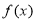 和
和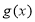 分别是
分别是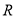 上的偶函数和奇函数,则下列结论恒成立的是( )
上的偶函数和奇函数,则下列结论恒成立的是( )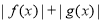 是偶函数 B.
是偶函数 B.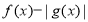 是奇函数
是奇函数 是偶函数 D.
是偶函数 D.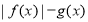 是奇函数
是奇函数