题目内容
12．已知函数f（x）=x（a-e-x），曲线y=f（x）上存在不同的两点，使得曲线在这两点处的切线都与y轴垂直，则实数a的取值范围是（ ）| A． | （-e2，+∞） | B． | （-e2，0） | C． | （-e-2，+∞） | D． | （-e-2，0） |
分析 由曲线y=f（x）上存在不同的两点，使得曲线在这两点处的切线都与y轴垂直，故f′（x）=a+（x-1）e-x=0有两个不同的解，即得a=（1-x）e-x有两个不同的解，即可解出a的取值范围．
解答 解：∵曲线y=f（x）上存在不同的两点，使得曲线在这两点处的切线都与y轴垂直，
∴f′（x）=a+（x-1）e-x=0有两个不同的解，即得a=（1-x）e-x有两个不同的解，
设y=（1-x）e-x，则y′=（x-2）e-x，∴x＜2，y′＜0，x＞2，y′＞0
∴x=2时，函数取得极小值-e-2，
∴0＞a＞-e-2．
故选D．
点评 本题主要考查了利用导数研究曲线上某点切线方程，函数零点等有关基础知识，考查运算求解能力、推理论证能力，考查化归与转化思想．
练习册系列答案
相关题目
20．某地农业监测部门统计发现：该地区近几年的生猪收购价格每四个月会重复出现，但生猪养殖成本逐月递增．下表是今年前四个月的统计情况：
现打算从以下两个函数模型：
①y=Asin（ωx+φ）+B，（A＞0，ω＞0，-π＜φ＜π），
②y=log2（x+a）+b
中选择适当的函数模型，分别来拟合今年生猪收购价格（元/斤）与相应月份之间的函数关系、养殖成本（元/斤）与相应月份之间的函数关系．
（1）请你选择适当的函数模型，分别求出这两个函数解析式；
（2）按照你选定的函数模型，帮助该部门分析一下，今年该地区生猪养殖户在8月和9月有没有可能亏损？
| 月份 | 1月份 | 2月份 | 3月份 | 4月份 |
| 收购价格（元/斤） | 6 | 7 | 6 | 5 |
| 养殖成本（元/斤） | 3 | 4 | 4.6 | 5 |
①y=Asin（ωx+φ）+B，（A＞0，ω＞0，-π＜φ＜π），
②y=log2（x+a）+b
中选择适当的函数模型，分别来拟合今年生猪收购价格（元/斤）与相应月份之间的函数关系、养殖成本（元/斤）与相应月份之间的函数关系．
（1）请你选择适当的函数模型，分别求出这两个函数解析式；
（2）按照你选定的函数模型，帮助该部门分析一下，今年该地区生猪养殖户在8月和9月有没有可能亏损？
17．过点P（2，-1）且倾斜角为$\frac{π}{4}$的直线方程是（ ）
| A． | x-y+1=0 | B． | $\sqrt{2}$x-2y-$\sqrt{2}$-2=0 | C． | x-y-3=0 | D． | $\sqrt{2}$x-2y+$\sqrt{2}$+1=0 |
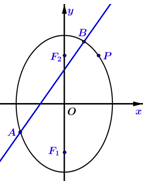设椭圆$M：\frac{y^2}{a^2}+\frac{x^2}{b^2}=1$（a＞b＞0）经过点$P（1，\sqrt{2}）$，其离心率与双曲线x2-y2=1的离心率互为倒数．