题目内容
3.已知cos($\frac{π}{12}$-θ)=$\frac{1}{3}$,则sin(2θ+$\frac{π}{3}$)=$-\frac{7}{9}$.分析 由已知求得cos($\frac{π}{6}-2θ$)的值,再由诱导公式得答案.
解答 解:∵cos($\frac{π}{12}$-θ)=$\frac{1}{3}$,
∴$cos(\frac{π}{6}-2θ)=2co{s}^{2}(\frac{π}{12}-θ)-1=2×\frac{1}{9}-1=-\frac{7}{9}$,
∴sin(2θ+$\frac{π}{3}$)=sin[$\frac{π}{2}$-($\frac{π}{6}-2θ$)]=cos($\frac{π}{6}-2θ$)=$-\frac{7}{9}$.
故答案为:-$\frac{7}{9}$.
点评 本题考查三角函数的化简求值,考查倍角公式及诱导公式的应用,是基础题.

练习册系列答案
相关题目
14.△ABC中,c=$\sqrt{3}$,b=1,∠B=30°,则△ABC的面积等于( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{4}$ | C. | $\frac{\sqrt{3}}{2}$或$\sqrt{3}$ | D. | $\frac{\sqrt{3}}{2}$或$\frac{\sqrt{3}}{4}$ |
11.若对任意实数x∈R,不等式$x_{\;}^2+m{x_{\;}}+2m-3≥0$恒成立,则实数m的取值范围是( )
| A. | [2,6] | B. | [-6,-2] | C. | (2,6) | D. | (-6,-2) |
18.要得到函数$y=sin(\frac{π}{4}-3x)$的图象,只需要将函数y=sin3x的图象( )m.
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
8.为了得到函数f(x)=sin(3x+$\frac{π}{4}$)的图象,只需将函数g(x)=sin3x的图象( )
| A. | 向右平移$\frac{π}{4}$个单位 | B. | 向左平移$\frac{π}{4}$个单位 | ||
| C. | 向右平移$\frac{π}{12}$个单位 | D. | 向左平移$\frac{π}{12}$个单位 |
12.已知函数f(x)=x(a-e-x),曲线y=f(x)上存在不同的两点,使得曲线在这两点处的切线都与y轴垂直,则实数a的取值范围是( )
| A. | (-e2,+∞) | B. | (-e2,0) | C. | (-e-2,+∞) | D. | (-e-2,0) |
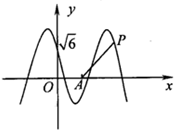 如图,函数y=2$\sqrt{3}$cos(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的图象与y轴交于点(0,$\sqrt{6}$),周期是π.
如图,函数y=2$\sqrt{3}$cos(ωx+φ)(ω>0,0≤φ≤$\frac{π}{2}$)的图象与y轴交于点(0,$\sqrt{6}$),周期是π.