题目内容
15.已知圆O的方程为x2+y2=4,过圆外一点P(3,$\sqrt{7}$)作圆O的两条切线,切点分别为T1和T2,则$\overrightarrow{P{T}_{1}}$•$\overrightarrow{P{T}_{2}}$=6.分析 根据直线与圆相切的性质可求PT1=PT2,及∠T1PT2,然后代入向量数量积的定义可求$\overrightarrow{P{T}_{1}}$•$\overrightarrow{P{T}_{2}}$.
解答 解:由题意,OT1=OT2=2,PO=4,
Rt△PT1O中,OT1=2,PO=4,PT1=2$\sqrt{3}$
∴∠OPT1=30°,∠T1PT2=2∠OPT1=60°
∴$\overrightarrow{P{T}_{1}}$•$\overrightarrow{P{T}_{2}}$=2$\sqrt{3}$$•2\sqrt{3}•\frac{1}{2}$=6
故答案为:6
点评 本题主要考查了圆的切线性质的应用及平面向量的数量积的定义的应用,属于基础试题.

练习册系列答案
相关题目
8.要得到函数 y=2cos x 的图象,只需将 y=2sin( x-$\frac{π}{3}$) 的图象( )
| A. | 向右平移$\frac{5π}{6}$个单位 | B. | 向右平移$\frac{π}{3}$个单位 | ||
| C. | 向左平移$\frac{5π}{6}$个单位 | D. | 向左平移$\frac{π}{3}$个单位 |
3.如果函数y=logax(a>0且a≠1)在[1,3]上的最大值与最小值的差为2,则满足条件的a值的集合是( )
| A. | $\{\sqrt{3}\}$ | B. | $\{\frac{{\sqrt{3}}}{3}\}$ | C. | $\{\frac{{\sqrt{3}}}{3},\sqrt{3}\}$ | D. | $\{\sqrt{3},3\}$ |
4.设双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$(a>0,b>0)的右焦点为F,过点F作x轴的垂线与双曲线交于B,C两点(点B在x轴上方),过点B作斜率为负数的渐近线的垂线,过点C作斜率为正数的渐近线的垂线,两垂线交于点D,若D到直线BC的距离等于虚轴长,则双曲线的离心率e等于( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
5.已知角α终边上一点P(-3,4),则cos(-π-α)的值为( )
| A. | -$\frac{4}{3}$ | B. | $\frac{4}{5}$ | C. | $\frac{3}{5}$ | D. | -$\frac{3}{5}$ |
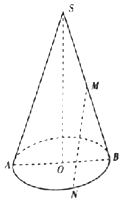 如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6.
如图,平面SAB为圆锥的轴截面,O为底面圆的圆心,M为母线SB的中点,N为底面圆周上的一点,AB=4,SO=6. 如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.
如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.