题目内容
20.${({\sqrt{x}-\frac{1}{x}})^5}$的二项展开式中x项的系数为-5.(用数字作答)分析 在二项展开式的通项公式中,令x的幂指数等于1,求出r的值,即可求得展开式中x项的系数.
解答 解:${({\sqrt{x}-\frac{1}{x}})^5}$的二项展开式的通项公式为 Tr+1=${C}_{5}^{r}$•(-1)r•${x}^{\frac{5-3r}{2}}$,令$\frac{5-3r}{2}$=1,求得r=1,
可得展开式中x项的系数为-${C}_{5}^{1}$=-5,
故答案为:-5.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,属于基础题.

练习册系列答案
相关题目
10.已知f(x)=$\frac{{2}^{x+1}+1}{{2}^{x}-1}$,且对于任意x∈[1,3],不等式f(x)>|x-2|+m恒成立,则m的取值范围是( )
| A. | (-∞,-4] | B. | (-$\frac{1}{2}$,+∞) | C. | (-∞,-$\frac{9}{8}$) | D. | (-∞,$\frac{10}{7}$) |
8.直线y=-2x+b一定通过( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二、四象限 | D. | 第二、三、四象限 |
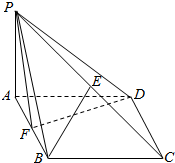 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=45°,AB=2,AD=$\sqrt{2}$,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,∠BAD=45°,AB=2,AD=$\sqrt{2}$,PA⊥平面ABCD,E是PC的中点,F是AB的中点.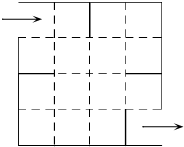 有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )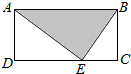 在长方形ABCD中,AB=3,BC=2,E为CD上一点,将一个质点随机投入长方形中,则质点落在阴影部分的概率为$\frac{1}{2}$.
在长方形ABCD中,AB=3,BC=2,E为CD上一点,将一个质点随机投入长方形中,则质点落在阴影部分的概率为$\frac{1}{2}$.