题目内容
4.若α∈(-$\frac{π}{2}$,0),cosα=$\frac{\sqrt{5}}{5}$,则tan(α-$\frac{π}{4}$)=3.分析 根据三角函数同角的关系式,求出tanα,然后利用两角和差的正切公式进行求解即可.
解答 解:∵α∈(-$\frac{π}{2}$,0),cosα=$\frac{\sqrt{5}}{5}$,
∴sinα=-$\sqrt{1-(\frac{\sqrt{5}}{5})^{2}}$=-$\sqrt{1-\frac{5}{25}}=-\sqrt{\frac{20}{25}}$=-$\frac{2\sqrt{5}}{5}$,
则tanα=$\frac{sinα}{cosα}$=$\frac{-\frac{2\sqrt{5}}{5}}{\frac{\sqrt{5}}{5}}$=-2,
则tan(α-$\frac{π}{4}$)=$\frac{tanα-tan\frac{π}{4}}{1+tanαtan\frac{π}{4}}$=$\frac{-2-1}{1-2}=\frac{-3}{-1}=3$,
故答案为:3.
点评 本题主要考查三角函数值的求解,利用三角函数的同角关系式以及两角和差的正切公式是解决本题的关键.

练习册系列答案
相关题目
14.设x∈R,则“x<1”是“x|x|<1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
12.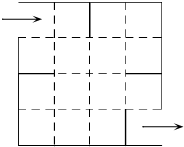 有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
 有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )
有一种走“方格迷宫”游戏,游戏规则是每次水平或竖直走动一个方格,走过的方格不能重复,只要有一个方格不同即为不同走法.现有如图的方格迷宫,图中的实线不能穿过,则从入口走到出口共有多少种不同走法?( )| A. | 6 | B. | 8 | C. | 10 | D. | 12 |
13.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=$\frac{{a}^{2}}{c}$交于点M,设其右焦点为F,且点F到渐近线的距离为d,则( )
| A. | |MF|>d | B. | |MF|<d | C. | |MF|=d | D. | 与a,b的值有关 |