题目内容
18.已知对称轴为坐标轴的双曲线的渐进线方程为y=±$\frac{b}{a}$x(a>0,b>0),若双曲线上有一点M(x0,y0),使b|x0|<a|y0|,则该双曲线的焦点( )| A. | 在x轴上 | B. | 在y轴上 | C. | 当a>b时,在x轴上 | D. | 当a>b时,在y轴上 |
分析 利用题设不等式,令二者平方,整理求得$\frac{{{y}_{0}}^{2}}{{b}^{2}}$-$\frac{{{x}_{0}}^{2}}{{a}^{2}}$>0,即可判断出焦点的位置.
解答 解:∵a|y0|>b|x0|≥0
∴平方a2y02>b2x02
∴$\frac{{{y}_{0}}^{2}}{{b}^{2}}$-$\frac{{{x}_{0}}^{2}}{{a}^{2}}$>0
∴焦点在y轴
故选:B.
点评 本题主要考查了双曲线的简单性质.考查了学生分析问题和解决问题的能力.

练习册系列答案
相关题目
8.直线y=-2x+b一定通过( )
| A. | 第一、三象限 | B. | 第二、四象限 | C. | 第一、二、四象限 | D. | 第二、三、四象限 |
13.双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一条渐近线与直线x=$\frac{{a}^{2}}{c}$交于点M,设其右焦点为F,且点F到渐近线的距离为d,则( )
| A. | |MF|>d | B. | |MF|<d | C. | |MF|=d | D. | 与a,b的值有关 |
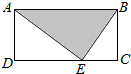 在长方形ABCD中,AB=3,BC=2,E为CD上一点,将一个质点随机投入长方形中,则质点落在阴影部分的概率为$\frac{1}{2}$.
在长方形ABCD中,AB=3,BC=2,E为CD上一点,将一个质点随机投入长方形中,则质点落在阴影部分的概率为$\frac{1}{2}$.