题目内容
4.已知复数z1满足|z1|=1,又z2=2i,则|z1+z2|的最大值是3.分析 |z1|=1,可设z1=cosθ+isinθ,z1+z2=cosθ+(sinθ+2)i,利用复数模的计算公式即可得出.
解答 解:∵|z1|=1,可设z1=cosθ+isinθ,
z1+z2=cosθ+(sinθ+2)i,
则|z1+z2|=$\sqrt{{cos}^{2}θ{+(sinθ+2)}^{2}}$=$\sqrt{5+4sinθ}$,
故1≤|z1+z2|≤3,
故答案为:3.
点评 本题考查了复数的运算法则、三角函数求值,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
9.已知F是双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点,过点F作E的一条渐近线的垂线,垂足为P,垂线PF与E相交于点Q,记点Q到E的两条渐近线的距离之积为d2,若|FP|=2d,则该双曲线的离心率( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
13.若向量$\vec a=(1,λ,2),\vec b=(2,-1,2)$,且$\vec a$与$\vec b$的夹角余弦为$\frac{8}{9}$,则λ等于( )
| A. | -2或$\frac{2}{55}$ | B. | -2 | C. | 2 | D. | 2或$-\frac{2}{55}$ |
14.若复数z满足z•i=2+3i,则在复平面内z对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
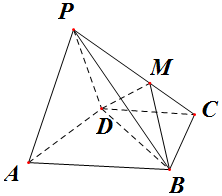 如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.
如图,在四棱锥P-ABCD中,AB∥CD,△PAD是等边三角形,平面PAD⊥平面ABCD,已知AD=2,$BD=2\sqrt{3}$,AB=2CD=4.