题目内容
4.已知数列{an},Sn是其前n项和,且满足2an=Sn+n(n∈N*).(1)求证:数列{an+1}是等比数列;
(2)设bn=log2(an+1),且Mn为数列{bn}的前n项和,求数列$\left\{{\frac{1}{M_n}}\right\}$的前n项和Tn.
分析 (1)利用数列递推关系、等比数列的定义即可证明.
(2)利用对数的运算性质、“裂项求和”方法即可得出.
解答 (l)证明:∵2an=Sn+n,∴a1=1,
当n≥2时,2an-1=Sn-1+n-1,即an=2an-1+1,
∴an+1=2an-1+1+1=2(an-1+1),
∴数列{an+1}是首项为2,公比为2的等比数列.
(2)解:由(1)知an+1=2•2n-1=2n,bn=log2(an+1)=n,
∴Mn=$\frac{{n({n+1})}}{2}$.
∴$\frac{1}{M_n}=\frac{2}{{n({n+1})}}=2({\frac{1}{n}-\frac{1}{n+1}})$,
故数列$\left\{{\frac{1}{M_n}}\right\}$的前n项和${T_n}=2[{({1-\frac{1}{2}})+({\frac{1}{2}-\frac{1}{3}})+…+({\frac{1}{n}-\frac{1}{n+1}})}]=2({1-\frac{1}{n+1}})=\frac{2n}{n+1}$.
点评 本题考査了等比数列的通项公式、“错位相减法”、对数运算性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.在数列{an}中,已知a1=0,an+2-an=2,则a7的值为( )
| A. | 9 | B. | 15 | C. | 6 | D. | 8 |
19.已知(3-4i)$\overline{z}$=i101(其中$\overline z$为z的共轭复数,i为虚数单位),则复数z的虚部为( )
| A. | $\frac{3i}{25}$ | B. | -$\frac{3}{25}$ | C. | $\frac{3}{25}$ | D. | -$\frac{4}{25}$ |
9.设θ是第四象限角,则点P(sin(sinθ),cos(sinθ))在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
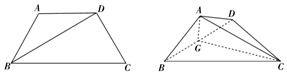 如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.
如图所示,在等腰梯形ABCD中,AD∥BC,AD=CD=AB,∠ABC=60°,将三角形ABD沿BD折起,使点A在平面BCD上的投影G落在BD上.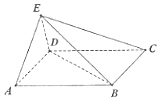 如图所示,在四棱锥E-ABCD中,ABCD是边长为2的正方形,且AE⊥平面CDE,且∠DAE=30°
如图所示,在四棱锥E-ABCD中,ABCD是边长为2的正方形,且AE⊥平面CDE,且∠DAE=30°