题目内容
2.设函数$f(x)=\frac{1}{3}a{x^3}+\frac{1}{2}b{x^2}+cx$(a,b,c∈R,a≠0)的图象在点(x,f(x))处的切线的斜率为k(x),且函数$g(x)=k(x)-\frac{1}{2}x$为偶函数.若函数k(x)满足下列条件:①k(-1)=0;②对一切实数x,不等式$k(x)≤\frac{1}{2}{x^2}+\frac{1}{2}$恒成立.(1)求函数k(x)的表达式;
(2)设函数$h(x)=ln{x^2}-(2m+3)x+\frac{12f(x)}{x}$(x>0)的两个极值点x1,x2(x1<x2)恰为φ(x)=lnx-sx2-tx的零点,当$m≥\frac{{3\sqrt{2}}}{2}$时,求$y=({x_1}-{x_2})φ'(\frac{{{x_1}+{x_2}}}{2})$的最小值.
分析 (1)由已知可得k(x)=f′(x)=ax2+bx+c,由函数$g(x)=k(x)-\frac{1}{2}x$为偶函数,g(-x)=g(x)恒成立,解得b=$\frac{1}{2}$.又k(-1)=0,可得a+c=$\frac{1}{2}$,由对一切实数x,不等式$k(x)≤\frac{1}{2}{x^2}+\frac{1}{2}$恒成立.可得(a-$\frac{1}{2}$)x2+$\frac{1}{2}$x+c-$\frac{1}{2}≤$0恒成立,因此$\left\{\begin{array}{l}{a-\frac{1}{2}<0}\\{△=\frac{1}{4}-4(a-\frac{1}{2})(c-\frac{1}{2})≤0}\end{array}\right.$,解出即可得出.
(2)由(1)得,f(x)=$\frac{1}{12}{x}^{3}$+$\frac{1}{4}$x2+$\frac{1}{4}$x,可得h(x)=2lnx+x2+3-2mx(x>0),h′(x)=$\frac{2}{x}$+2x-2m=$\frac{2({x}^{2}-mx+1)}{x}$,由题意得$\left\{\begin{array}{l}{△={m}^{2}-4>0}\\{{x}_{1}+{x}_{2}=m}\\{{x}_{1}{x}_{2}=1}\end{array}\right.$,又$m≥\frac{{3\sqrt{2}}}{2}$,可得$0<\frac{{x}_{1}}{{x}_{2}}≤\frac{1}{2}$,由x1,x2(x1<x2)恰为φ(x)=lnx-sx2-tx的零点,代入两式相减得,ln$\frac{{x}_{1}}{{x}_{2}}$-s(x1-x2)(x1+x2)-t(x1-x2)=0,代入$y=({x_1}-{x_2})φ'(\frac{{{x_1}+{x_2}}}{2})$=$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$--ln$\frac{{x}_{1}}{{x}_{2}}$.设n=$\frac{{x}_{1}}{{x}_{2}}$($0<n≤\frac{1}{2}$),y=$\frac{2(n-1)}{n+1}$-lnn($0<n≤\frac{1}{2}$),记为M(n),利用导数研究其单调性极值与最值即可得出.
解答 解:(1)由已知可得k(x)=f′(x)=ax2+bx+c,
∵函数$g(x)=k(x)-\frac{1}{2}x$为偶函数,∴g(-x)=k(-x)-$\frac{1}{2}$(-x)=k(x)-$\frac{1}{2}$x,
即ax2-bx+c+$\frac{1}{2}$x=ax2+bx+c-$\frac{1}{2}$x恒成立,所以b=$\frac{1}{2}$.
又k(-1)=0,∴$a-\frac{1}{2}$+c=0,即a+c=$\frac{1}{2}$,
又∵对一切实数x,不等式$k(x)≤\frac{1}{2}{x^2}+\frac{1}{2}$恒成立.
∴(a-$\frac{1}{2}$)x2+$\frac{1}{2}$x+c-$\frac{1}{2}≤$0恒成立,
∴$\left\{\begin{array}{l}{a-\frac{1}{2}<0}\\{△=\frac{1}{4}-4(a-\frac{1}{2})(c-\frac{1}{2})≤0}\end{array}\right.$,
∴a=c=$\frac{1}{4}$,∴k(x)=$\frac{1}{4}$x2+$\frac{1}{2}$x+$\frac{1}{4}$.
(2)由(1)得,f(x)=$\frac{1}{12}{x}^{3}$+$\frac{1}{4}$x2+$\frac{1}{4}$x,
∴h(x)=2lnx+x2+3-2mx(x>0),
h′(x)=$\frac{2}{x}$+2x-2m=$\frac{2({x}^{2}-mx+1)}{x}$,
由题意得$\left\{\begin{array}{l}{△={m}^{2}-4>0}\\{{x}_{1}+{x}_{2}=m}\\{{x}_{1}{x}_{2}=1}\end{array}\right.$,又$m≥\frac{{3\sqrt{2}}}{2}$,
∴m2=$\frac{({x}_{1}+{x}_{2})^{2}}{{x}_{1}{x}_{2}}$≥$\frac{9}{2}$,解得$0<\frac{{x}_{1}}{{x}_{2}}≤\frac{1}{2}$,
∵x1,x2(x1<x2)恰为φ(x)=lnx-sx2-tx的零点,
∴φ(x1)=lnx1-s${x}_{1}^{2}$-tx1=0,φ(x2)=lnx2-$s{x}_{2}^{2}$-tx2=0,
两式相减得,ln$\frac{{x}_{1}}{{x}_{2}}$-s(x1-x2)(x1+x2)-t(x1-x2)=0,又φ′(x)=$\frac{1}{x}$-2sx-t,
从而$y=({x_1}-{x_2})φ'(\frac{{{x_1}+{x_2}}}{2})$=(x1-x2)$[\frac{2}{{x}_{1}+{x}_{2}}-s({x}_{1}+{x}_{2})-t]$=$\frac{2({x}_{1}-{x}_{2})}{{x}_{1}+{x}_{2}}$-ln$\frac{{x}_{1}}{{x}_{2}}$=$\frac{2(\frac{{x}_{1}}{{x}_{2}}-1)}{\frac{{x}_{1}}{{x}_{2}}+1}$--ln$\frac{{x}_{1}}{{x}_{2}}$.
设n=$\frac{{x}_{1}}{{x}_{2}}$($0<n≤\frac{1}{2}$),
则y=$\frac{2(n-1)}{n+1}$-lnn($0<n≤\frac{1}{2}$),记为M(n),
M′(n)=$2×\frac{n+1-(n-1)}{(n+1)^{2}}$-$\frac{1}{n}$=$\frac{-(n-1)^{2}}{n(n+1)^{2}}$<0,
∴M(n)在$(0,\frac{1}{2}]$上单调递减,
∴M(n)min=M$(\frac{1}{2})$=ln2-$\frac{2}{3}$,
∴求$y=({x_1}-{x_2})φ'(\frac{{{x_1}+{x_2}}}{2})$的最小值为ln2-$\frac{2}{3}$.
点评 本题考查了利用导数研究其单调性极值与最值、导数的几何意义、分类讨论方法、函数的奇偶性、换元方法,考查了推理能力与计算能力,属于难题.

| A. | $({-\frac{5π}{12},\frac{π}{12}})$ | B. | $({\frac{π}{12},\frac{7π}{12}})$ | C. | $({-\frac{π}{6},\frac{π}{3}})$ | D. | $({-\frac{π}{12},\frac{5π}{12}})$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
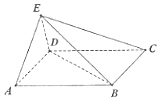 如图所示,在四棱锥E-ABCD中,ABCD是边长为2的正方形,且AE⊥平面CDE,且∠DAE=30°
如图所示,在四棱锥E-ABCD中,ABCD是边长为2的正方形,且AE⊥平面CDE,且∠DAE=30°