题目内容
已知函数f(x)=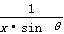 +ln x在[1,+∞)上为增函数,且θ∈(0,π),g(x)=tx-
+ln x在[1,+∞)上为增函数,且θ∈(0,π),g(x)=tx-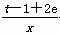 -ln x,t∈R.
-ln x,t∈R.
(1)求θ的值;
(2)当t=0时,求函数g(x)的单调区间和极大值;
(3)若在[1,e]上至少存在一个x0,使得g(x0)>f(x0)成立,求t的取值范围.
解:(1)由已知得f ′(x)=- ≥0在[1,+∞)上恒成立,即
≥0在[1,+∞)上恒成立,即 ≥0在[1,+∞)上恒成立,∵θ∈(0,π),∴sin θ>0,∴sin θ·x-1≥0在[1,+∞)上恒成立,只需sin θ·1-1≥0,即sin θ≥1,∴sin θ=1,由θ∈(0,π),知θ=
≥0在[1,+∞)上恒成立,∵θ∈(0,π),∴sin θ>0,∴sin θ·x-1≥0在[1,+∞)上恒成立,只需sin θ·1-1≥0,即sin θ≥1,∴sin θ=1,由θ∈(0,π),知θ= .
.
(2)∵t=0,∴g(x)=- -ln x,x∈(0,+∞),
-ln x,x∈(0,+∞),
∴g′(x)=
令g′(x)=0,则x=2e-1∈(0,+∞),∴x,g′(x)和g(x)的变化情况如下表:
| x | (0,2e-1) | 2e-1 | (2e-1,+∞) |
| g′(x) | + | 0 | - |
| g(x) | ↗ | 极大值 | ↘ |

练习册系列答案
相关题目
 ,B=
,B= ,则A∩B=( )
,则A∩B=( ) B.(2,3]C.[1,2) D.(1,2)
B.(2,3]C.[1,2) D.(1,2)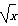 (0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式.
(0<x≤1),求x∈[-5,-4]时,函数f(x)的解析式. ,都存在x∈R,使得f(x)<m
,都存在x∈R,使得f(x)<m

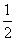 e2x-ax(a∈R,e为自然对数的底数).
e2x-ax(a∈R,e为自然对数的底数). e2x+x2+x在区间(0,+∞)上为增函数,求整数m的最大值.
e2x+x2+x在区间(0,+∞)上为增函数,求整数m的最大值.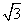 )2+lg
)2+lg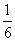 +lg 0.06;
+lg 0.06;