题目内容
已知函数f(x)是定义在R上的奇函数，且它的图象关于直线x＝1对称．
(1)求证：f(x)是周期为4的周期函数；
(2)若f(x)＝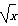
(0<x≤1)，求x∈[－5，－4]时，函数f(x)的解析式．
解：(1)证明：由函数f(x)的图象关于直线x＝1对称，
有f(x＋1)＝f(1－x)，即有f(－x)＝f(x＋2)．
又函数f(x)是定义在R上的奇函数，
故有f(－x)＝－f(x)，故f(x＋2)＝－f(x)．
从而f(x＋4)＝－f(x＋2)＝f(x)，
即f(x)是周期为4的周期函数．
(2)由函数f(x)是定义在R上的奇函数，有f(0)＝0.x∈[－1,0)时，－x∈(0,1]，f(x)＝－f(－x)＝－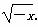
.
故x∈[－1,0]时，f(x)＝－.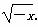
x∈[－5，－4]时，x＋4∈[－1,0]，
f(x)＝f(x＋4)＝－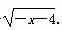
.
从而，x∈[－5，－4]时，函数f(x)＝－.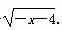
练习册系列答案
相关题目
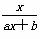(a≠0)，f(2)＝1，又方程f(x)＝x有惟一解，求f(x)的解析式．
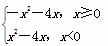，若f(a－2)＋f(a)>0，则实数a的取值范围是( )
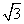或a>－1＋
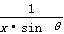＋ln x在[1，＋∞)上为增函数，且θ∈(0，π)，g(x)＝tx－
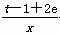－ln x，t∈R.