题目内容
在△ABC中，角A，B，C所对的边分别为a，b，c，若a=4，b=2，cosA=
，则sinB的值为 ．
| 1 |
| 3 |
考点：余弦定理
专题：三角函数的求值
分析：由cosA的值，利用同角三角函数间基本关系求出sinA的值，再由a与b的值，利用正弦定理求出sinB的值即可．
解答：
解：∵△ABC中，cosA=
，
∴sinA=
=
，
∵a=4，b=2，
∴由正弦定理
=
得：sinB=
=
=
．
故答案为：
．
| 1 |
| 3 |
∴sinA=
| 1-cos2A |
2
| ||
| 3 |
∵a=4，b=2，
∴由正弦定理
| a |
| sinA |
| b |
| sinB |
| bsinA |
| a |
2×
| ||||
| 4 |
| ||
| 3 |
故答案为：
| ||
| 3 |
点评：此题考查了正弦定理，以及同角三角函数间的基本关系，熟练掌握正弦定理是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
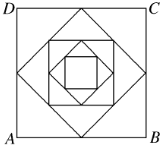如图，正方形ABCD的边长是a，依次连接正方形ABCD各边中点得到一个新的正方形，再依次连接新正方形各边中点又得到一个新的正方形，依此得到一系列的正方形，如图所示．现有一只小虫从A点出发，沿正方形的边逆时针方向爬行，每遇到新正方形的顶点时，沿这个正方形的边逆时针方向爬行，如此下去，问爬行2n条线段的长度的平方和是多少？