题目内容
已知函数f（x）=ex-1，则f（x）=0处的切线方程为 ．
考点：利用导数研究曲线上某点切线方程
专题：计算题,导数的概念及应用
分析：求出函数的导函数，把x=0代入导函数求出的函数值即为切线方程的斜率，把x=0代入函数解析式中得到切点的纵坐标，进而确定出切点坐标，根据求出的斜率和切点坐标写出切线方程即可．
解答：
解：由题意得：f′（x）=ex，把x=0代入得：f′（0）=1，即切线方程的斜率k=1，
且把x=0代入函数解析式得：y=0，即切点坐标为（0，0），
则所求切线方程为：y=x．
故答案为：y=x．
且把x=0代入函数解析式得：y=0，即切点坐标为（0，0），
则所求切线方程为：y=x．
故答案为：y=x．
点评：此题考查学生会利用导数求曲线上过某点切线方程的斜率，是一道基础题．
练习册系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
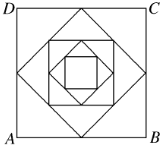如图，正方形ABCD的边长是a，依次连接正方形ABCD各边中点得到一个新的正方形，再依次连接新正方形各边中点又得到一个新的正方形，依此得到一系列的正方形，如图所示．现有一只小虫从A点出发，沿正方形的边逆时针方向爬行，每遇到新正方形的顶点时，沿这个正方形的边逆时针方向爬行，如此下去，问爬行2n条线段的长度的平方和是多少？
复数z=
的虚部是（ ）
| 1+2i |
| 1-i |
A、
| ||
B、
| ||
C、-
| ||
D、-
|