题目内容
5．在棱长为2的正方体ABCD-A1B1C1D1中任取一点M，则满足∠AMB＞90°的概率为（ ）| A． | $\frac{π}{24}$ | B． | $\frac{π}{12}$ | C． | $\frac{π}{8}$ | D． | $\frac{π}{6}$ |
分析 在棱长为2的正方体ABCD-A1B1C1D1中任取一点M，满足∠AMB＞90°的区域的面积为半径为1的球体的$\frac{1}{4}$，以体积为测度，即可得出结论．
解答 解：在棱长为2的正方体ABCD-A1B1C1D1中任取一点M，满足∠AMB＞90°的区域的面积为半径为1的球体的$\frac{1}{4}$，体积为$\frac{1}{4}•\frac{4}{3}•π•{1}^{3}$=$\frac{π}{3}$，
∴所求概率为$\frac{\frac{π}{3}}{8}$=$\frac{π}{24}$，
故选：A．
点评 本题考查几何概型的概率计算，关键是确定满足条件的区域，利用体积比值求解．
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
相关题目
3．对$?x∈（\;0\;，\;\frac{1}{3}\;）$，23x≤logax+1恒成立，则实数a的取值范围是（ ）
| A． | $（\;0\;，\;\frac{2}{3}\;）$ | B． | $（\;0\;，\;\frac{1}{2}\;]$ | C． | $[\;\frac{1}{3}\;，\;1\;）$ | D． | $[\;\frac{1}{2}\;，\;1\;）$ |
16．若一个圆柱的正视图与其侧面展开图是相似矩形，则这个圆柱的全面积与侧面积之比为（ ）
| A． | $1+\sqrt{π}$ | B． | 1+$\frac{1}{{\sqrt{π}}}$ | C． | $1+\frac{1}{{\sqrt{2π}}}$ | D． | $1+\frac{1}{{2\sqrt{π}}}$ |
17．下列结论正确的是（ ）
| A． | 命题“如果p2+q2=2，则p+q≤2”的否命题是“如果p+q＞2，则p2+q2≠2” | |
| B． | 命题p：?x∈[0，1]，ex≥1，命题q：?x∈R，x2+x+1＜0，则p∨q为假 | |
| C． | “若am2＜bm2，则a＜b”的逆命题为真命题 | |
| D． | 若${（\sqrt{x}-\frac{1}{{2\root{3}{x}}}）^n}$的展开式中第四项为常数项，则n=5 |
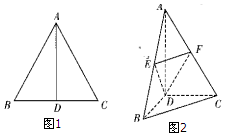如图，边长为2的等边三角形ABC中，D为BC的中点，将△ABC沿AD翻折成直二面角B-AD-C，点E，F分别是AB，AC的中点．