题目内容
11.直线kx-y+1-2k=0,当k变动时,所有直线都过定点( )| A. | (0,0) | B. | (0,1) | C. | (3,1) | D. | (2,1) |
分析 先把参数k分离出来,再令k的系数等于零,求得x、y的值,可得直线经过定点的坐标.
解答 解:∵kx-y+1-2k=0,即k(x-2)-y+1=0,令x-2=0,可得y=1,
故直线kx-y+1-2k=0经过定点(2,1),
故选:D.
点评 本题主要考查直线经过定点问题,属于基础题.

练习册系列答案
相关题目
18.已知x≥0,y≥0,x2+y2=4,μ=x•y-4(x+y)+10,μ的最值情况是( )
| A. | 有最大值2,最小值2(2-$\sqrt{2}$)2 | B. | 有最大值2,最小值0 | ||
| C. | 有最大值10,最小值2(2-$\sqrt{2}$)2 | D. | 最值不存在 |
6.如图,ABCD-A1B1C1D1为正方体,则下列结论错误的是( )
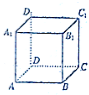

| A. | A1C⊥B1D1 | B. | B1D1∥平面BDC1 | ||
| C. | A1C⊥平面BDC1 | D. | 异面直线AD与BC1所成的角为30° |
16.已知如图:

则a81的位置是( )

则a81的位置是( )
| A. | 第13行第2个数 | B. | 第14行第3个数 | C. | 第13行第3个数 | D. | 第17行第2个数 |
3.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x(x-1),则x<0时,f(x)的解析式为( )
| A. | f(x)=x(x+1) | B. | f(x)=-x(x+1) | C. | f(x)=x(1-x) | D. | f(x)=x2-1 |
1.已知函数f(x)=loga(-x2+log2ax)对任意x∈(0,$\frac{1}{2}$)都有意义,则实数a的取值范围是( )
| A. | [$\frac{1}{128}$,$\frac{1}{2}$) | B. | [$\frac{1}{64}$,$\frac{1}{2}$) | C. | [$\frac{1}{32}$,$\frac{1}{2}$) | D. | [$\frac{1}{16}$,$\frac{1}{2}$) |
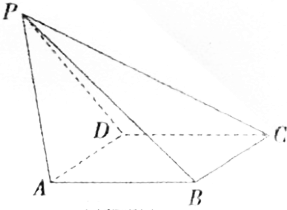 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.