题目内容
20.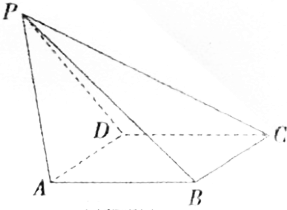 如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.
如图,已知四棱锥P-ABCD,侧面PAD为边长等于2的正三角形,底面ABCD为菱形,∠BDA=60°.(1)证明:BC⊥PB;
(2)若PB=3,求点P到平面ABCD的距离.
分析 (1)取AD的中点,连接OP,OB,利用线面垂直的判定定理可得AD⊥平面POB,又BC∥AD,可得BC⊥平面POB,即可证明BC⊥PB.
(2)设点P到平面ABCD的距离为h,由(1)可得:AD⊥平面POB,点A到平面POB的距离是AO=1.利用VP-BOD=VB-POD,即可解出.
解答 (1)证明:取AD的中点,连接OP,OB,由已知可得:OP⊥AD,OB⊥AD,又OP∩OB=O,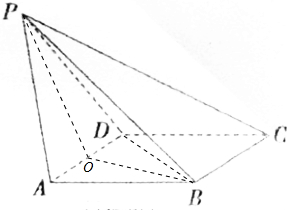
∴AD⊥平面POB,
∵BC∥AD,∴BC⊥平面POB,
∵PB?平面POB,∴BC⊥PB.
(2)解:设点P到平面ABCD的距离为h,由(1)可得:AD⊥平面POB,点A到平面POB的距离是AO=1.
在△POB中,PO=BO=$\sqrt{3}$,PB=3,
∴S△POB=$\frac{1}{2}×\frac{\sqrt{3}}{2}$×3=$\frac{3\sqrt{3}}{4}$.
由VP-BOD=VB-POD,
可得:$\frac{1}{3}h×\frac{1}{2}×1×\sqrt{3}$=$\frac{1}{3}×1×\frac{3\sqrt{3}}{4}$,可得h=$\frac{3}{2}$.
点评 本题考查了线面面面垂直与平行的判定与性质定理、等积变形,考查了空间想象能力、推理能力与计算能力,属于中档题.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
11.直线kx-y+1-2k=0,当k变动时,所有直线都过定点( )
| A. | (0,0) | B. | (0,1) | C. | (3,1) | D. | (2,1) |
10.下列函数中,y的最小值为2的是( )
| A. | y=x+$\frac{1}{x}$ | B. | y=x2+$\frac{1}{x^2}$ | C. | y=lgx+$\frac{1}{lgx}$ | D. | y=sinx+$\frac{1}{sinx}$ | ||||
| E. | y=x2+$\frac{1}{x^2}$ |
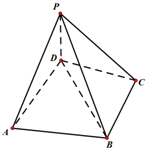 如图,四棱锥P-ABCD中,底面ABCD为四边形,△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,平面PBD⊥平面ABCD.
如图,四棱锥P-ABCD中,底面ABCD为四边形,△ABD是边长为2的正三角形,BC⊥CD,BC=CD,PD⊥AB,平面PBD⊥平面ABCD.