题目内容
10.甲、乙两人约定在下午 4:30:5:00 间在某地相见,且他们在 4:30:5:00 之间 到达的时刻是等可能的,约好当其中一人先到后一定要等另一人 20 分钟,若另一人仍不到则可以离去,则这两人能相见的概率是( )| A. | $\frac{3}{4}$ | B. | $\frac{8}{9}$ | C. | $\frac{7}{16}$ | D. | $\frac{11}{12}$ |
分析 由题意知本题是一个几何概型,试验发生包含的所有事件对应的集合是Ω:{(x,y)|0≤x≤30,0≤y≤30},做出集合对应的面积是边长为30的正方形的面积,写出满足条件的事件对应的集合和面积,根据面积之比得到概率
解答 解:因为两人谁也没有讲好确切的时间,
故样本点由两个数(甲乙两人各自到达的时刻)组成.
以4:30点钟作为计算时间的起点建立如图所示的平面直角坐标系,设甲乙各在第x分钟和第y分钟到达,则样本空间为Ω:{(x,y)|0≤x≤30,0≤y≤30},画成图为一正方形.
会面的充要条件是|x-y|≤20,即事件A={可以会面}所对应的区域是图中的阴影线部分,
∴由几何概型公式知所求概率为面积之比,即P(A)=$\frac{3{0}^{2}-1{0}^{2}}{3{0}^{2}}=\frac{8}{9}$;
故选B.
点评 本题的难点是把时间分别用x,y坐标来表示,从而把时间长度这样的一维问题转化为平面图形的二维面积问题,转化成面积型的几何概型问题.

练习册系列答案
相关题目
20.下列说法正确的是( )
| A. | 类比推理、归纳推理、演绎推理都是合情推理 | |
| B. | 合情推理得到的结论一定是正确的 | |
| C. | 合情推理得到的结论不一定正确 | |
| D. | 归纳推理得到的结论一定是正确的 |
5.若复数z满足z(4-i)=5+3i(i为虚数单位),则复数z的共轭复数为( )
| A. | 1-i | B. | -1+i | C. | 1+i | D. | -1-i |
20.已知函数f(x)=x$({{e^x}-\frac{1}{e^x}})$,若f(x1)<f(x2),则( )
| A. | x1>x2 | B. | x1<x2 | C. | ${x}_{1}^{2}$<${x}_{2}^{2}$ | D. | x1+x2=0 |
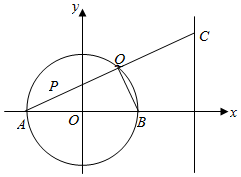 已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.
已知圆O:x2+y2=9,直线l1:x=6,圆O与x轴相交于点A,B(如图),点P(-1,2)是圆O内一点,点Q为圆O上任一点(异于点A、B),直线AQ与l1相交于点C.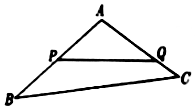 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.