题目内容
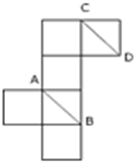将正方体纸盒展开如图所示，直线AB、CD在原正方体中的位置是（ ）| A、异面成60° | B、垂直 |
| C、相交成60° | D、平行 |
考点：空间中直线与直线之间的位置关系
专题：空间位置关系与距离
分析：把已知条件中的正方体纸盒的展开图，还原正方体，能够求出结果．
解答：
解：由正方体纸盒的展开图，
还原正方体，如图，
得到线段AB、CD是相邻的两个面内的两条不相交的对角线，
∴直线AB、CD在原正方体中的位置是异面直线，
连结ED，EC，得到ED∥AB，△DCE是等边三角形，
∴这两条异面直线所成的角是60°．
故选：A．
还原正方体，如图，
得到线段AB、CD是相邻的两个面内的两条不相交的对角线，
∴直线AB、CD在原正方体中的位置是异面直线，
连结ED，EC，得到ED∥AB，△DCE是等边三角形，
∴这两条异面直线所成的角是60°．
故选：A．
点评：本题考查空间中两条直线的位置关系，是基础题，解题时要熟练掌握正方体的平面展开图．
练习册系列答案
阅读快车系列答案
相关题目
阅读程序框图，若输入m=4，n=6，则输出a，i分别是（ ）
| A、a=12，i=3 |
| B、a=12，i=4 |
| C、a=8，i=3 |
| D、a=8，i=4 |
已知
=（1，1），
=（4，1），
=（4，5），则
与
夹角的余弦值为（ ）
| OA |
| OB |
| OC |
| AB |
| AC |
A、
| ||
B、
| ||
| C、0 | ||
| D、以上结果都不对 |
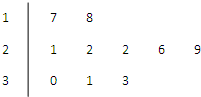如图是某公司10个销售店某月销售某产品数量（单位：台）的茎叶图，则数据落在区间[20，30）内的概率为（ ）| A、0.2 | B、0.4 |
| C、0.5 | D、0.6 |
下列四个函数中，在（0，+∞）上为增函数的是（ ）
| A、f（x）=3-x | ||
| B、f（x）=x2-3x | ||
C、f（x）=
| ||
| D、f（x）=|x| |
已知数列{an}是等差数列，a1=1，公差d≠0，若a1，a2，a5成等比数列，则a8=（ ）
| A、10 | B、15 | C、13 | D、14 |
若函数f（x）=loga（x2-ax+3）在区间（-∞，
）上是减函数，则a的取值范围是（ ）
| a |
| 2 |
| A、（0，1） | ||
| B、（1，+∞） | ||
C、（1，2
| ||
D、（1，2
|