题目内容
阅读程序框图，若输入m=4，n=6，则输出a，i分别是（ ）
| A、a=12，i=3 |
| B、a=12，i=4 |
| C、a=8，i=3 |
| D、a=8，i=4 |
考点：程序框图
专题：阅读型,图表型,算法和程序框图
分析：由程序框图依次计算第一、第二、第三次运行的结果，直到满足条件满足a被6整除，结束运行，输出此时a、i的值．
解答：
解：由程序框图得：
第一次运行i=1，a=4；
第二次运行i=2，a=8；
第三次运行i=3，a=12；满足a被6整除，结束运行，输出a=12，i=3．
故选A．
第一次运行i=1，a=4；
第二次运行i=2，a=8；
第三次运行i=3，a=12；满足a被6整除，结束运行，输出a=12，i=3．
故选A．
点评：本题考查了直到型循环结构的程序框图，解答的关键是读懂程序框图．
练习册系列答案
高效智能课时作业系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
一个物体的运动方程为s=-t+t2，其中s的单位是米，t的单位是秒，那么物体在3秒末的瞬时速度是（ ）
| A、8米/秒 | B、7米/秒 |
| C、6米/秒 | D、5米/秒 |
tan（-1560°）的值为（ ）
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是（ ）
| A、若α⊥β，m?α，n?β，则m⊥n |
| B、若m⊥α，m∥n，n∥β，则α⊥β |
| C、若m⊥n，m?α，n?β，则α⊥β |
| D、若α∥β，m?α，n?β，则m∥n |
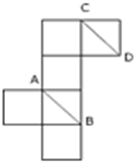将正方体纸盒展开如图所示，直线AB、CD在原正方体中的位置是（ ）| A、异面成60° | B、垂直 |
| C、相交成60° | D、平行 |
已知函数f（x）=|log4x|，正实数m、n满足m＜n，且f（m）=f（n），若f（x）在区间[m5，n]上的最大值为5，则m、n的值分别为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|