题目内容
已知数列{an}是等差数列，a1=1，公差d≠0，若a1，a2，a5成等比数列，则a8=（ ）
| A、10 | B、15 | C、13 | D、14 |
考点：等比数列的性质,等差数列的性质
专题：等差数列与等比数列
分析：根据等差数列的通项公式以及等比中项的性质，建立方程即可求出公差，然后进行计算即可．
解答：
解：∵数列{an}是等差数列，
∴由a1，a2，a5成等比数列得：
a1a5=（a2）2，
即a1(a1+4d)=(a1+d)2，
即2a1d=d2，
∴d=2a1=2，
∴a8=a1+7d=1+2×7=15，
故选：B
∴由a1，a2，a5成等比数列得：
a1a5=（a2）2，
即a1(a1+4d)=(a1+d)2，
即2a1d=d2，
∴d=2a1=2，
∴a8=a1+7d=1+2×7=15，
故选：B
点评：本题主要考查等差数列和等比数列的定义和运算，要求熟练掌握相应的通项公式．
练习册系列答案
相关题目
设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是（ ）
| A、若α⊥β，m?α，n?β，则m⊥n |
| B、若m⊥α，m∥n，n∥β，则α⊥β |
| C、若m⊥n，m?α，n?β，则α⊥β |
| D、若α∥β，m?α，n?β，则m∥n |
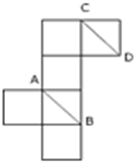将正方体纸盒展开如图所示，直线AB、CD在原正方体中的位置是（ ）| A、异面成60° | B、垂直 |
| C、相交成60° | D、平行 |
函数f(x)=
+
的定义域为（ ）
| 1 |
| x-1 |
| 2+x |
| A、[-2，+∞） |
| B、[-2，1）∪（1，+∞） |
| C、R |
| D、（-∞，-2] |
函数y=
-sin2x-3cosx的最小值是（ ）
| 5 |
| 4 |
A、-
| ||
| B、-2 | ||
C、
| ||
D、-
|
已知向量
与
的夹角为120°，且|
|=2，|
|=3，若
=λ
+
，且
⊥
，则实数λ的值为（ ）
| AB |
| AC |
| AB |
| AC |
| AP |
| AB |
| AC |
| AP |
| BC |
A、
| ||
| B、13 | ||
| C、6 | ||
D、
|
已知函数f（x）=|log4x|，正实数m、n满足m＜n，且f（m）=f（n），若f（x）在区间[m5，n]上的最大值为5，则m、n的值分别为（ ）
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
执行如图所示的程序框图，输出的S值为64则“ ”处应填（ ）| A、2 | B、3 | C、4 | D、5 |