题目内容
若函数f(x)=loga(x2-ax+3)在区间(-∞,
)上是减函数,则a的取值范围是( )
| a |
| 2 |
| A、(0,1) | ||
| B、(1,+∞) | ||
C、(1,2
| ||
D、(1,2
|
考点:复合函数的单调性
专题:函数的性质及应用
分析:内层函数g(x)=x2-ax+3在区间(-∞,
)上是减函数,由复合函数的单调性知,外层函数y=logag(x)为增函数,得到a的初步范围,再由g(x)=x2-ax+3在区间(-∞,
)上大于0恒成立求出a的范围,取交集后求得实数a的取值范围.
| a |
| 2 |
| a |
| 2 |
解答:
解:由对数式的底数大于0且不等于1知,a>0且a≠1.
令g(x)=x2-ax+3,函数的对称轴方程为x=
,
函数g(x)=x2-ax+3在(-∞,
)上为减函数,在(
,+∞)上为增函数,
要使复合函数f(x)=loga(x2-ax+3)在区间(-∞,
)上是减函数,
则外层函数y=logag(x)为增函数,且同时满足内层函数g(x)=x2-ax+3在(-∞,
)上大于0恒成立,
即
,
解得:1<a≤2
.
∴使函数f(x)=loga(x2-ax+3)在区间(-∞,
)上是减函数的a的取值范围是(1,2
].
故选:C.
令g(x)=x2-ax+3,函数的对称轴方程为x=
| a |
| 2 |
函数g(x)=x2-ax+3在(-∞,
| a |
| 2 |
| a |
| 2 |
要使复合函数f(x)=loga(x2-ax+3)在区间(-∞,
| a |
| 2 |
则外层函数y=logag(x)为增函数,且同时满足内层函数g(x)=x2-ax+3在(-∞,
| a |
| 2 |
即
|
解得:1<a≤2
| 3 |
∴使函数f(x)=loga(x2-ax+3)在区间(-∞,
| a |
| 2 |
| 3 |
故选:C.
点评:本题考查复合函数的单调性,复合的两个函数同增则增,同减则减,一增一减则减,注意对数函数的定义域是求解的前提,考查学生发现问题解决问题的能力,是中档题.

练习册系列答案
相关题目
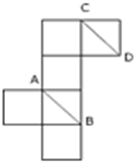 将正方体纸盒展开如图所示,直线AB、CD在原正方体中的位置是( )
将正方体纸盒展开如图所示,直线AB、CD在原正方体中的位置是( )| A、异面成60° | B、垂直 |
| C、相交成60° | D、平行 |
函数y=
-sin2x-3cosx的最小值是( )
| 5 |
| 4 |
A、-
| ||
| B、-2 | ||
C、
| ||
D、-
|
已知向量
与
的夹角为120°,且|
|=2,|
|=3,若
=λ
+
,且
⊥
,则实数λ的值为( )
| AB |
| AC |
| AB |
| AC |
| AP |
| AB |
| AC |
| AP |
| BC |
A、
| ||
| B、13 | ||
| C、6 | ||
D、
|
计算cos(-
)=( )
| 16π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
已知函数f(x)=|log4x|,正实数m、n满足m<n,且f(m)=f(n),若f(x)在区间[m5,n]上的最大值为5,则m、n的值分别为( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
一个几何体的三视图如图所示,则该几何体的体积为( )


A、
| ||
B、
| ||
| C、3 | ||
| D、4 |
二进制数111111(2)化成十进制数的值是( )
| A、63 | B、62 | C、64 | D、61 |