题目内容

已知
OA
=（1，1），
OB
=（4，1），
OC
=（4，5），则
AB
与
AC
夹角的余弦值为（　　）
A、
4
5
B、
3
5
C、0
D、以上结果都不对
考点：平面向量数量积的坐标表示、模、夹角
专题：平面向量及应用
分析：利用向量的夹角公式即可得出．
解答： 解：∵
AB
=
OB
-
OA
=（4，1）-（1，1）=（3，0），
AC
=
OC
-
OA
=（4，5）-（1，1）=（3，4）．
∴
AB
•
AC
=（3，0）•（3，4）=9
∴cos＜
AB
，
AC
＞=
AB
•
AC
|
AB
| |
AC
|
=
9
3×
32+42
=
3
5
．
故选：B．
点评：本题考查了向量的夹角公式、数量积运算，属于基础题．
练习册系列答案
相关题目
已知函数f（x）=
3x2-4，x＞0
1，x≤0
，则f（f（0））=
 
．
已知直线m、n、l不重合，平面α、β不重合，下列命题正确的有
 

（1）若m?β，n?β，m∥α，n∥α，则α∥β
（2）若m?β，n?β，l⊥m，l⊥n，则l⊥β
（3）若α⊥β，m?α，n?β，则m⊥n；
（4）若m⊥α，m∥n，则n⊥α
tan（-1560°）的值为（　　）
A、-
3
B、-
3
3
C、
3
3
D、
3
设m，n是两条不同的直线，α，β是两个不同的平面，下列命题中正确的是（　　）
A、若α⊥β，m?α，n?β，则m⊥n
B、若m⊥α，m∥n，n∥β，则α⊥β
C、若m⊥n，m?α，n?β，则α⊥β
D、若α∥β，m?α，n?β，则m∥n
设α∥β，P∈α，Q∈β，当P、Q分别在平面α、β内运动时，线段PQ的中点X也随着运动，则所有的动点X（　　）
A、不共面
B、当且仅当P、Q分别在两条平行直线上移动时才共面
C、当且仅当P、Q分别在两条互相垂直的异面直线上移动时才共面
D、无论P、Q如何运动都共面
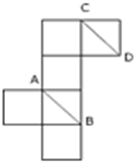将正方体纸盒展开如图所示，直线AB、CD在原正方体中的位置是（　　）
A、异面成60°B、垂直
C、相交成60°D、平行
函数y=
5
4
-sin2x-3cosx的最小值是（　　）
A、-
7
4
B、-2
C、
1
4
D、-
5
4
一个几何体的三视图如图所示，则该几何体的体积为（　　）
A、
9
2
B、
7
2
C、3
D、4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网