题目内容
下列四个函数中,在(0,+∞)上为增函数的是( )
| A、f(x)=3-x | ||
| B、f(x)=x2-3x | ||
C、f(x)=
| ||
| D、f(x)=|x| |
考点:函数单调性的判断与证明
专题:函数的性质及应用
分析:根据选项中的函数单调性特征,判定是否满足在(0,+∞)上为增函数即可.
解答:
解:A中,f(x)=3-x在定义域R上是减函数,∴不满足题意;
B中,f(x)=x2-3x在(-∞,
)上是减函数,在(
,+∞)上是增函数,∴不满足题意;
C中,f(x)=
在(-∞,0)和(0,+∞)上是减函数,∴不满足题意;
D中,f(x)=|x|在(-∞,0)上是减函数,在(0,+∞)上是增函数,∴满足题意;
故选:D.
B中,f(x)=x2-3x在(-∞,
| 3 |
| 2 |
| 3 |
| 2 |
C中,f(x)=
| 1 |
| x |
D中,f(x)=|x|在(-∞,0)上是减函数,在(0,+∞)上是增函数,∴满足题意;
故选:D.
点评:本题考查了基本初等函数的单调性问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
tan(-1560°)的值为( )
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
设α∥β,P∈α,Q∈β,当P、Q分别在平面α、β内运动时,线段PQ的中点X也随着运动,则所有的动点X( )
| A、不共面 |
| B、当且仅当P、Q分别在两条平行直线上移动时才共面 |
| C、当且仅当P、Q分别在两条互相垂直的异面直线上移动时才共面 |
| D、无论P、Q如何运动都共面 |
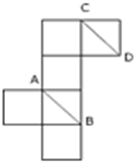 将正方体纸盒展开如图所示,直线AB、CD在原正方体中的位置是( )
将正方体纸盒展开如图所示,直线AB、CD在原正方体中的位置是( )| A、异面成60° | B、垂直 |
| C、相交成60° | D、平行 |
如图的程序框图输出的结果为( )


| A、511 | B、254 |
| C、1022 | D、510 |
函数y=
-sin2x-3cosx的最小值是( )
| 5 |
| 4 |
A、-
| ||
| B、-2 | ||
C、
| ||
D、-
|
计算cos(-
)=( )
| 16π |
| 3 |
A、-
| ||||
B、
| ||||
C、-
| ||||
D、
|
设y=x2•ex,则y′等于( )
| A、x2ex+2x |
| B、2xex |
| C、(2x+x2)ex |
| D、(x+x2)•ex |