题目内容
设P是双曲线x2-
=1的右支上的动点，F为双曲线的右焦点，已知A（3，1），则|PA|+|PF|的最小值为 ．
| y2 |
| 3 |
考点：双曲线的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：设双曲线左焦点为F2，根据双曲线的定义可知|PA|+|PF|=|PF2|-2a+|PA|，进而可知当P、F2、A三点共线时有最小值，根据双曲线方程可求F2的坐标，此时|PF2|+|PA|=|AF2|，利用两点间的距离公式求得答案．
解答：
解：设双曲线左焦点为F2，
由双曲线的定义可得|PF2|-|PF|=2a，即|PF|=|PF2|-2a，
则|PA|+|PF|=|PF2|+|PA|-2a≥|F2A|-2a，
当P、F2、A三点共线时，|PF2|+|PA|有最小值，
此时F2（-2，0）、A（3，1），
则|PF2|+|PA|=|AF2|=
，
而对于这个双曲线，2a=2，
所以最小值为
-2．
故答案为：
-2．
由双曲线的定义可得|PF2|-|PF|=2a，即|PF|=|PF2|-2a，
则|PA|+|PF|=|PF2|+|PA|-2a≥|F2A|-2a，
当P、F2、A三点共线时，|PF2|+|PA|有最小值，
此时F2（-2，0）、A（3，1），
则|PF2|+|PA|=|AF2|=
| 26 |
而对于这个双曲线，2a=2，
所以最小值为
| 26 |
故答案为：
| 26 |
点评：本题主要考查了双曲线的定义，考查了两点的距离公式，运用两点间线段最短是解题的关键．
练习册系列答案
导学教程高中新课标系列答案
相关题目
已知函数y=f（x）是定义域为R的偶函数．当x≥0时，f（x）=
，若关于x的方程5[f（x）]2-（5a+6）f（x）+6a=0（a∈R），有且仅有6个不同实数根，则实数a的取值范围是（ ）
|
A、0＜a＜1或a=
| ||
B、0≤a≤1或a=
| ||
C、0＜a≤1或a=
| ||
D、1＜a≤
|
若椭圆的中心及两个焦点将两条准线之间的距离四等分，则椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
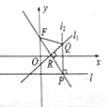如图，在平面直角坐标系xOy中，点F（0，1），直线l：y=-1，点P在直线l上移动，R是线段PF与x轴的交点，过点R，P分别作直线l1，l2，使得l1⊥PF，l2⊥l，l1∩l2=Q．设数列{an}的前n项和为Sn，且a1=a2=1，{nSn+（n+2）an}为等差数列，则an=（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|