题目内容
已知集合P={x|2012≤x≤2013}，Q={x|a-1≤x≤a}，若P⊆Q，实数a的取值集合为 ．
考点：集合的包含关系判断及应用
专题：集合
分析：根据集合P={x|2012≤x≤2013}，Q={x|a-1≤x≤a}，P⊆Q，构造关于a的不等式组，解不等式组可得答案．
解答：
解：依题意得
，∴2013≤a≤2013．
∴a=2013，所以实数a的集合为{2013}．
故答案为：{2013}．
|
∴a=2013，所以实数a的集合为{2013}．
故答案为：{2013}．
点评：本题考查的知识点是集合的包含关系判断及应用，其中根据集合包含的定义，构造关于a的不等式组，是解答的关键．
练习册系列答案
阅读快车系列答案
相关题目
函数f（x）=x2-2tx-4（t∈R）在闭区间[0，1]上的最小值记为g（t）．则g（t）的函数解析式（ ）
A、g（t）=
| ||||||
| B、g（t）=-t2+2 | ||||||
| C、g（t）=-t2+2t | ||||||
| D、g（t）=-t2+2t+2 |
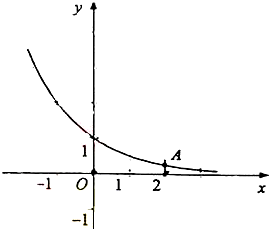如图，函数f（x）=ax（a＞0，a≠1）的图象经过点A（2，