题目内容
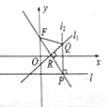 如图,在平面直角坐标系xOy中,点F(0,1),直线l:y=-1,点P在直线l上移动,R是线段PF与x轴的交点,过点R,P分别作直线l1,l2,使得l1⊥PF,l2⊥l,l1∩l2=Q.
如图,在平面直角坐标系xOy中,点F(0,1),直线l:y=-1,点P在直线l上移动,R是线段PF与x轴的交点,过点R,P分别作直线l1,l2,使得l1⊥PF,l2⊥l,l1∩l2=Q.(1)求动点Q的轨迹C的方程;
(2)设N为轨迹C上的动点,是否在y轴上存在定点E,使得以NE为直径的圆被直线y=3截得的弦长恒为定值?若存在,求出定点E和弦长;若不存在,请说明理由.
考点:直线与圆锥曲线的综合问题,轨迹方程
专题:圆锥曲线中的最值与范围问题
分析:(1)由题意可得R是线段PF的中点,且QR⊥PF,可得|QP|=|QF|,由抛物线的定义可得:动点Q的轨迹C是以点F为焦点,直线l为准线的抛物线,即可得出轨迹C的方程.
(2)假设在y轴上存在定点E,使得以NE为直径的圆被直线y=3截得的弦长恒为定值.设以NE为直径的圆被直线y=3截得的弦为GH,设N(x,y),E(0,t),则圆心为M(
,
),圆心M到直线y=3的距离d=|
-3|.圆M的半径R=
|NE|=
,及x2=4y,可得|GH|=2
=2
,令t=4,即可得出.
(2)假设在y轴上存在定点E,使得以NE为直径的圆被直线y=3截得的弦长恒为定值.设以NE为直径的圆被直线y=3截得的弦为GH,设N(x,y),E(0,t),则圆心为M(
| x |
| 2 |
| t+y |
| 2 |
| t+y |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| x2+(y-t)2 |
| R2-d2 |
| (4-t)y+3t-9 |
解答:
解:(1)由题意可得R是线段PF的中点,且QR⊥PF,
∴|QP|=|QF|,
∴动点Q的轨迹C是以点F为焦点,直线l为准线的抛物线,
∴轨迹C的方程为x2=4y.
(2)假设在y轴上存在定点E,使得以NE为直径的圆被直线y=3截得的弦长恒为定值.
设以NE为直径的圆被直线y=3截得的弦为GH,
设N(x,y),E(0,t),则圆心为M(
,
),
圆心M到直线y=3的距离d=|
-3|=
|t+y-6|.
圆M的半径R=
|NE|=
,
∵x2=4y,
∴R=
,
∴|GH|=2
=2
=2
,
令t=4,则|GH|=2
为定长,定点为E(0,4).
因此在y轴上存在定点E(0,4),使得以NE为直径的圆被直线y=3截得的弦长为2
恒为定值.
∴|QP|=|QF|,
∴动点Q的轨迹C是以点F为焦点,直线l为准线的抛物线,
∴轨迹C的方程为x2=4y.
(2)假设在y轴上存在定点E,使得以NE为直径的圆被直线y=3截得的弦长恒为定值.
设以NE为直径的圆被直线y=3截得的弦为GH,
设N(x,y),E(0,t),则圆心为M(
| x |
| 2 |
| t+y |
| 2 |
圆心M到直线y=3的距离d=|
| t+y |
| 2 |
| 1 |
| 2 |
圆M的半径R=
| 1 |
| 2 |
| 1 |
| 2 |
| x2+(y-t)2 |
∵x2=4y,
∴R=
| 1 |
| 2 |
| 4y+(y-t)2 |
∴|GH|=2
| R2-d2 |
|
| (4-t)y+3t-9 |
令t=4,则|GH|=2
| 3 |
因此在y轴上存在定点E(0,4),使得以NE为直径的圆被直线y=3截得的弦长为2
| 3 |
点评:本题考查了抛物线的定义及其标准方程性质、圆的标准方程及其性质、直线与圆的相交弦长公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
下列条件中,能判断两个平面平行的是( )
| A、一个平面内的一条直线平行于另一个平面 |
| B、一个平面内的两条直线平行于另一个平面 |
| C、一个平面内有无数条直线平行于另一个平面 |
| D、一个平面内的任何一条直线都平行于另一个平面 |
 将全体正偶数排成一个三角数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为
将全体正偶数排成一个三角数阵:按照以上排列的规律,第n行(n≥3)从左向右的第3个数为