题目内容
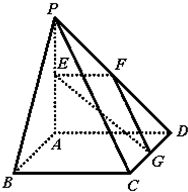 如图,四棱锥P-ABCD中,底面ABCD为正方形,PA⊥AD,面PAD⊥面ABCD,PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,
如图,四棱锥P-ABCD中,底面ABCD为正方形,PA⊥AD,面PAD⊥面ABCD,PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,(1)求证:PB∥面EFG;
(2)求异面直线EG与BD所成角的余弦;
(3)线段CD上是否存在点Q,使A到平面EFQ的距离为0.8?若存在,求出CQ长,若不存在,请说明理由.
考点:异面直线及其所成的角,直线与平面平行的判定
专题:空间位置关系与距离,空间角
分析:(1)以A为原点,AB为x轴,AD为y轴,AP为z轴,建立空间直角坐标系,利用向量法能证明PB∥平面EFG.
(2)由
=(1,2,-1),
=(-2,2,0),利用向量法能求出异面直线EG与BD所成角的余弦值.
(3)假设线段CD上存在点Q,使A到平面EFQ的距离为0.8,设CQ长为t,则Q(2-t,2,0),由此利用向量法能推导出线段CD上不存在点Q,使A到平面EFQ的距离为0.8.
(2)由
| EG |
| BD |
(3)假设线段CD上存在点Q,使A到平面EFQ的距离为0.8,设CQ长为t,则Q(2-t,2,0),由此利用向量法能推导出线段CD上不存在点Q,使A到平面EFQ的距离为0.8.
解答:
(1)证明:以A为原点,AB为x轴,AD为y轴,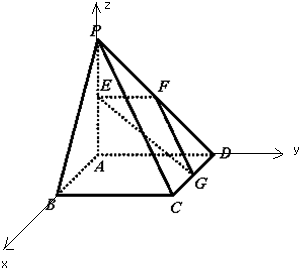
AP为z轴,建立空间直角坐标系,
则P(0,0,2),B(2,0,0),E(0,0,1),
D(0,2,0),F(0,1,1),G(1,2,0),
=(2,0,-2),
=(0,1,0),
=(1,2,-1),
设平面EFG的法向量
=(x,y,z),
则
,
取x=1,得
=(1,0,1),
∵
•
=2+0-2=0,PB不包含于平面EFG,
∴PB∥平面EFG.
(2)解:
=(1,2,-1),
=(-2,2,0),
|cos<
,
>|=|
|=
.
∴异面直线EG与BD所成角的余弦值为
.
(3)解:假设线段CD上存在点Q,使A到平面EFQ的距离为0.8,
设CQ长为t,则Q(2-t,2,0),
=(0,1,0),
=(2-t,2,-1),
设平面EFQ的法向量
=(a,b,c),
则
,取a=1,得
=(1,0,2-t),
∵
=(0,0,1),A到平面EFQ的距离为0.8,
∴
=
=0.8,
整理,得39t2+36t+20=0,
△=362-80×39<0,
∴t不存在,即线段CD上不存在点Q,使A到平面EFQ的距离为0.8.

AP为z轴,建立空间直角坐标系,
则P(0,0,2),B(2,0,0),E(0,0,1),
D(0,2,0),F(0,1,1),G(1,2,0),
| PB |
| EF |
| EG |
设平面EFG的法向量
| m |
则
|
取x=1,得
| m |
∵
| PB |
| m |
∴PB∥平面EFG.
(2)解:
| EG |
| BD |
|cos<
| EG |
| BD |
| -2+4+0 | ||||
|
| ||
| 6 |
∴异面直线EG与BD所成角的余弦值为
| ||
| 6 |
(3)解:假设线段CD上存在点Q,使A到平面EFQ的距离为0.8,
设CQ长为t,则Q(2-t,2,0),
| EF |
| EQ |
设平面EFQ的法向量
| n |
则
|
| n |
∵
| AE |
∴
|
| ||||
|
|
| |2-t| | ||
|
整理,得39t2+36t+20=0,
△=362-80×39<0,
∴t不存在,即线段CD上不存在点Q,使A到平面EFQ的距离为0.8.
点评:本题考查直线与平面平行的证明,考查异面直线所成角的余弦值的求法,考查线段CD上是否存在点Q,使A到平面EFQ的距离为0.8的判断与求法,解题时要注意向量法的合理运用.

练习册系列答案
相关题目
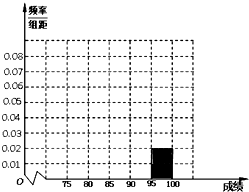 某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.
某校高三年级在高校自主招生期间,把学生的平时成绩按“百分制”折算并排序,选出前300名学生,并对这300名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列.