题目内容
已知二次函数g(x)对任意的x都满足g(x-1)+g(1-x)=x2-2x-1,且g(1)=-1,设函数f(x)=g(x+
)+mlnx+
.
(1)求g(x)的表达式;
(2)是否存在实数m∈(-∞,0),使得对任意的x∈R+,恒有f(x)>0,若存在,求出实数m的取值范围;若不存在请说明理由.
| 1 |
| 2 |
| 9 |
| 8 |
(1)求g(x)的表达式;
(2)是否存在实数m∈(-∞,0),使得对任意的x∈R+,恒有f(x)>0,若存在,求出实数m的取值范围;若不存在请说明理由.
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)设g(x)=ax2+bx+c(a≠0),于是g(x-1)+g(1-x)=2a(x-1)2+2c=(x-1)2-2,g(1)=-1,由此能求出g(x)的表达式.
(2)f(x)=g(x+
)+mlnx+
=
x2+mlnx(m∈R,x>0),当m>0时,由对数函数性质,f(x)的值域为R;当m=0时,f(x)=
>0对?x>0,f(x)>0恒成立;当m<0时,由f′(x)=x+
=0,得x=
.由此利用导数性质能求出存在实数m∈(-e,0],使得对任意的x∈R+,恒有f(x)>0.
(2)f(x)=g(x+
| 1 |
| 2 |
| 9 |
| 8 |
| 1 |
| 2 |
| x2 |
| 2 |
| m |
| x |
| -m |
解答:
解:(1)设g(x)=ax2+bx+c(a≠0),
于是g(x-1)+g(1-x)=2a(x-1)2+2c=(x-1)2-2,
所以a=
,c=-1,
又g(1)=-1,则b=-
,
所以g(x)=
x2-
x-1.
(2)f(x)=g(x+
)+mlnx+
=
x2+mlnx(m∈R,x>0),
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,f(x)=
>0对?x>0,f(x)>0恒成立;
当m<0时,由f′(x)=x+
=0,得x=
,
列表如下:
这时,[f(x)]min=f(
)=-
+mln
,
由[f(x)]min>0,得
,解得-e<m<0,
若?x>0,f(x)>0恒成立,则实数m的取值范围是(-e,0].
所以,存在实数m∈(-e,0],使得对任意的x∈R+,恒有f(x)>0.
于是g(x-1)+g(1-x)=2a(x-1)2+2c=(x-1)2-2,
所以a=
| 1 |
| 2 |
又g(1)=-1,则b=-
| 1 |
| 2 |
所以g(x)=
| 1 |
| 2 |
| 1 |
| 2 |
(2)f(x)=g(x+
| 1 |
| 2 |
| 9 |
| 8 |
| 1 |
| 2 |
当m>0时,由对数函数性质,f(x)的值域为R;
当m=0时,f(x)=
| x2 |
| 2 |
当m<0时,由f′(x)=x+
| m |
| x |
| -m |
列表如下:
| x | (0,
|
| (
| ||||||
| f′(x) | - | 0 | + | ||||||
| f(x) | ↓ | 极小值 | ↑ |
| -m |
| m |
| 2 |
| -m |
由[f(x)]min>0,得
|
若?x>0,f(x)>0恒成立,则实数m的取值范围是(-e,0].
所以,存在实数m∈(-e,0],使得对任意的x∈R+,恒有f(x)>0.
点评:本题考查函数的表达式的求法,考查满足条件的实数的取值范围是否存在的判断与求法,是中档题,解题时要注意导数性质的合理运用.

练习册系列答案
相关题目
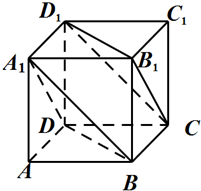 如图,在正方体ABCD-A1B1C1D1中.
如图,在正方体ABCD-A1B1C1D1中.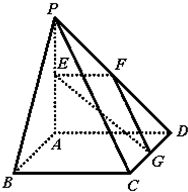 如图,四棱锥P-ABCD中,底面ABCD为正方形,PA⊥AD,面PAD⊥面ABCD,PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,
如图,四棱锥P-ABCD中,底面ABCD为正方形,PA⊥AD,面PAD⊥面ABCD,PA=AD=2,E,F,G分别是线段PA,PD,CD的中点, 如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影恰好是AB的中点O,底面ABC是正三角形,其重心为G点,D是BC中点,B1D交BC1于E.
如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影恰好是AB的中点O,底面ABC是正三角形,其重心为G点,D是BC中点,B1D交BC1于E.