题目内容
已知函数f（x）=
，
（1）化简f（x）；
（2）求f（-
）的值．
sin(-x+
| ||||
| tan(-x-π)sin(x-3π) |
（1）化简f（x）；
（2）求f（-
| 13π |
| 3 |
考点：运用诱导公式化简求值
专题：三角函数的求值
分析：（1）f（x）解析式利用诱导公式化简，计算即可得到结果；
（2）把x=-
代入计算即可求出f（-
）的值．
（2）把x=-
| 13π |
| 3 |
| 13π |
| 3 |
解答：
解：（1）f（x）=
=-cosx；
（2）f（-
）=-cos（-
）=-cos
=-cos（4π+
）=-cos
=-
．
| cosx(-sinx)tanx |
| -tanx(-sinx) |
（2）f（-
| 13π |
| 3 |
| 13π |
| 3 |
| 13π |
| 3 |
| π |
| 3 |
| π |
| 3 |
| 1 |
| 2 |
点评：此题考查了运用诱导公式化简求值，熟练掌握诱导公式是解本题的关键．
练习册系列答案
相关题目
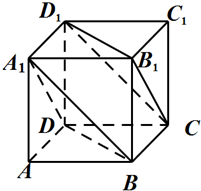如图，在正方体ABCD-A1B1C1D1中．
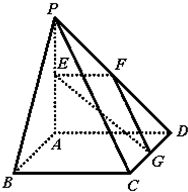如图，四棱锥P-ABCD中，底面ABCD为正方形，PA⊥AD，面PAD⊥面ABCD，PA=AD=2，E，F，G分别是线段PA，PD，CD的中点，
如图，在斜三棱柱ABC-A1B1C1中，点A1在底面ABC上的射影恰好是AB的中点O，底面ABC是正三角形，其重心为G点，D是BC中点，B1D交BC1于E．