题目内容
已知函数f(x)=
(1)判断f(x)的奇偶性;
(2)求函数f(x)在x∈[0,5]上的最大值和最小值.
| 2x-1 |
| x+1 |
(1)判断f(x)的奇偶性;
(2)求函数f(x)在x∈[0,5]上的最大值和最小值.
考点:函数奇偶性的判断,函数的最值及其几何意义
专题:函数的性质及应用
分析:(1)首先求出定义域为{x|x≠-1},关于原点不对称;是非奇非偶的函数;
(2)将函数变形,分离变量得到f(x)=2-
,在x∈[0,5]上是增函数,所以x=0时取最小值,x=5时取最大值.
(2)将函数变形,分离变量得到f(x)=2-
| 3 |
| x+1 |
解答:
解:(1)首先求出定义域为{x|x≠-1},关于原点不对称;是非奇非偶的函数;
(2)由已知,f(x)=
=2-
,在x∈[0,5]上是增函数,所以x=0时取最小值f(0)=-1,x=5时取最大值f(5)=
.
(2)由已知,f(x)=
| 2x-1 |
| x+1 |
| 3 |
| x+1 |
| 3 |
| 2 |
点评:本题考查了函数奇偶性的判定以及函数值域的求法;
要判定函数的奇偶性,必须首先判断定义域是否关于原点对称,如果定义域关于原点不对称,则函数是非奇非偶的函数;如果对称,再利用奇偶性的定义判断.
要判定函数的奇偶性,必须首先判断定义域是否关于原点对称,如果定义域关于原点不对称,则函数是非奇非偶的函数;如果对称,再利用奇偶性的定义判断.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
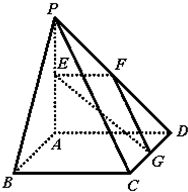 如图,四棱锥P-ABCD中,底面ABCD为正方形,PA⊥AD,面PAD⊥面ABCD,PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,
如图,四棱锥P-ABCD中,底面ABCD为正方形,PA⊥AD,面PAD⊥面ABCD,PA=AD=2,E,F,G分别是线段PA,PD,CD的中点,

 如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影恰好是AB的中点O,底面ABC是正三角形,其重心为G点,D是BC中点,B1D交BC1于E.
如图,在斜三棱柱ABC-A1B1C1中,点A1在底面ABC上的射影恰好是AB的中点O,底面ABC是正三角形,其重心为G点,D是BC中点,B1D交BC1于E.