题目内容
4.点P在双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右支上,其左、右焦点分别为F1,F2,直线PF1与以坐标原点O为圆心,a为半径的圆相切于点A,线段PF1的垂直平分线恰好过点F2,则$\frac{{S}_{△O{F}_{1}A}}{{S}_{△P{F}_{1}{F}_{2}}}$的值为$\frac{1}{8}$.分析 根据相似三角形的性质分别求得D和A的纵坐标,根据三角形的面积公式,即可求得答案.
解答 解:由题意,线段PF1的垂直平分线恰过点F2,垂直为D,AD为△F1F2D的中位线,
则yD=2yA=$\frac{1}{2}$yp,yA=$\frac{1}{4}$yp,
∴$\frac{{S}_{△O{F}_{1}A}}{{S}_{△P{F}_{1}{F}_{2}}}$=$\frac{\frac{1}{2}•c•{y}_{A}}{\frac{1}{2}•2c•{y}_{D}}$=$\frac{1}{8}$,
则$\frac{{S}_{△O{F}_{1}A}}{{S}_{△P{F}_{1}{F}_{2}}}$=$\frac{1}{8}$,
故答案为:$\frac{1}{8}$.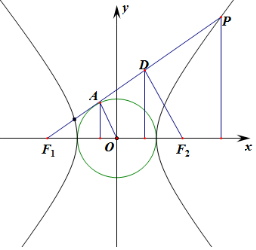
点评 本题考查三角形面积的计算,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目