题目内容
19.已知{an}是等差数列,其前n项和为Sn,{bn}是等比数列,且a1=b1=2,a4+b4=27,S4-b4=10.(1)求数列{an}与{bn}的通项公式;
(2)求Tn=a1b1+a2b2+…+anbn的值.
分析 (1)利用等差数列与等比数列的通项公式即可得出.
(2)利用“错位相减法”与等比数列的求和公式即可得出.
解答 解:(1)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
由a1=b1=2,得a4=2+3d,b4=2q3,S4=8+6d,
由条件得方程组$\left\{\begin{array}{l}2+3d+2{q^3}=27\\ 8+6d-2{q^3}=10\end{array}$,
解得:$\left\{\begin{array}{l}d=3\\ q=2\end{array}$,故an=3n-1,bn=2n(n∈N*).
(2)Tn=2×2+5×22+8×23+…+(3n-1)×2n,①
2Tn=2×22+5×23+8×24+…+(3n-1)×2n+1,②
①-②,得:-Tn=2×2+3×22+3×23+…+3×2n-(3n-1)×2n+1,
∴Tn=8-8×2n+3n×2n+1.
点评 本题考査了等差数列与等比数列的通项公式与求和公式、“错位相减法”,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知偶函数f(x)在区间(-∞,0]内单调递减,a=f(log23),b=f(log45),$c=f({2^{\frac{1}{2}}})$,则a,b,c满足( )
| A. | a<b<c | B. | c<a<b | C. | b<a<c | D. | c<b<a |
11.直线x=a分别与曲线y=2(x+1),y=x+lnx交于A、B两点,则|AB|的最小值为( )
| A. | 3 | B. | 2 | C. | $\frac{3\sqrt{2}}{4}$ | D. | $\frac{3}{2}$ |
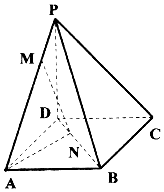 如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.
如图,四棱锥P-ABCD底面为正方形,已知PD⊥平面ABCD,PD=AD,点M为线段PA上任意一点(不含端点),点N在线段BD上,且PM=DN.