题目内容
13.等差数列{an}的各项均为正数,a1=1,前n项和为Sn;数列{bn}为等比数列,b1=1,且b2S2=6,b2+S3=8.(1)求数列{an}与{bn}的通项公式;
(2)求{an•bn}的前n项和Tn.
分析 (1)设等差数列{an}的公差为d,d>0,{bn}的公比为q,运用等差数列和等比数列的通项公式和求和公式,解方程可得公差和公比,即可得到所求通项公式;
(2)求得an•bn=n•2n-1.运用数列的求和方法:错位相减法,结合等比数列的求和公式,化简整理即可得到所求和.
解答 解:(1)设等差数列{an}的公差为d,d>0,{bn}的公比为q,
则an=1+(n-1)d,bn=qn-1.
由b2S2=6,b2+S3=8,
有q(2+d)=6,q+3+3d=8,
解得d=1,q=2,或q=9,d=-$\frac{4}{3}$(舍去),
故an=n,bn=2n-1.
(2)an•bn=n•2n-1.
前n项和为Tn=1•20+2•21+3•22+…+n•2n-1,
2Tn=1•21+2•22+3•23+…+n•2n.
两式相减可得-Tn=1+21+22+…+2n-1-n•2n
=$\frac{1-{2}^{n}}{1-2}$-n•2n.
化简可得Tn=1+(n-1)•2n.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查方程思想,以及数列的求和方法:错位相减法,考查化简整理的运算能力,属于中档题.

练习册系列答案
相关题目
1.已知i是虚数单位,复数z满足z(3+4i)=1+i,则复平面内表示z的共轭复数的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
18.在区间[0,1]上随机选取两个数x和y,则y>2x的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{3}$ |
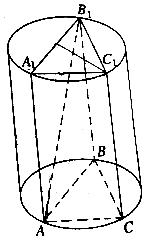 如图,圆柱有一个高6$\sqrt{2}$cm,体积为54$\sqrt{6}$cm3的内接正三棱柱ABC-A1B1C1.
如图,圆柱有一个高6$\sqrt{2}$cm,体积为54$\sqrt{6}$cm3的内接正三棱柱ABC-A1B1C1.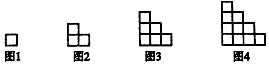 如图图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第15个图形中小正方形的个数是120.
如图图形由小正方形组成,请观察图1至图4的规律,并依此规律,写出第15个图形中小正方形的个数是120.