题目内容
已知[x]表示不超过实数x的最大整数（x∈R），如：[-1.3]=-2，[0.8]=0，[3.4]=3．定义F（x）=x-[x]，给出如下命题：
①使[x+1]=3成立的x的取值范围是2≤x＜3；
②函数F（x）的定义域为R，值域为[0，1]；
③F（
）+F（
）+F（
）+…+F（
）=1007；
④设函数G（x）=
，则函数y=G（x）-|sinx|，x∈[-π，π]的不同零点有7个．
其中正确的命题的序号为 ．
①使[x+1]=3成立的x的取值范围是2≤x＜3；
②函数F（x）的定义域为R，值域为[0，1]；
③F（
| 2013 |
| 2014 |
| 20132 |
| 2014 |
| 20133 |
| 2014 |
| 20132014 |
| 2014 |
④设函数G（x）=
|
其中正确的命题的序号为
考点：进行简单的合情推理
专题：推理和证明
分析：①由题意知[x+1]=3时，有
解得即可；
②由题意[x]≤x＜[x]+1，得x-[x]的取值范围，即{x}的值域；
③对于F（
）=
，F（
）=
，…F（
）=
，计算即可
④由题意0≤f（x）＜1，讨论0≤x＜1，x≥1和x＜0时，y=G（x）-|sinx|，x∈[-π，π]的零点情况．
|
②由题意[x]≤x＜[x]+1，得x-[x]的取值范围，即{x}的值域；
③对于F（
| 2013 |
| 2014 |
| 2013 |
| 2014 |
| 20132 |
| 2014 |
| 1 |
| 2014 |
| 20132014 |
| 2014 |
| 1 |
| 2014 |
④由题意0≤f（x）＜1，讨论0≤x＜1，x≥1和x＜0时，y=G（x）-|sinx|，x∈[-π，π]的零点情况．
解答：
解：对于①∵[x+1]=3，有
，解得2≤x＜3，故①正确
对于②∵[x]≤x＜[x]+1，∴0≤x-[x]＜1，函数{x}的值域是[0，1），故②错误；
对于③F（
）=
，F（
）=F(
)=F(2014-2+
)=
，F（
）=F（2020142-3×2014+3-
）=F（-
）=
+，…，F（
）=
所以F（
）+F（
）+F（
）+…+F（
）=
+
+
+…+
=1007；，故③正确
对于④当0≤x＜1时，G（x）=x+[x]=x+0=x，当1≤x＜2，则G（x）=x-1，
当2≤x＜3，则G（x）=x-2，
当3≤x＜4，则G（x）=x-3
…
当-1≤x＜0，则0≤x+1＜1，则G（x）=G（x+1）=x+1，
当-2≤x＜-1，则-1≤x+1＜0，则G（x）=G（x+1）=x+2，
当-3≤x＜-2，则-2≤x+1＜-1，则G（x）=G（x+1）=x+3，…
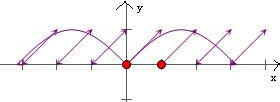
令y=0，则G（x）=|sinx|，在同一个坐标系中，画出函数y=G（x）和
y=|sinx|的图象，显然有7个交点，故④正确．
故其中正确的命题的序号为①③④．
故答案为：①③④
|
对于②∵[x]≤x＜[x]+1，∴0≤x-[x]＜1，函数{x}的值域是[0，1），故②错误；
对于③F（
| 2013 |
| 2014 |
| 2013 |
| 2014 |
| 20132 |
| 2014 |
| (2014-1)2 |
| 2014 |
| 1 |
| 2014 |
| 1 |
| 2014 |
| 20133 |
| 2014 |
| 1 |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 2014 |
| 20132014 |
| 2014 |
| 1 |
| 2014 |
所以F（
| 2013 |
| 2014 |
| 20132 |
| 2014 |
| 20133 |
| 2014 |
| 20132014 |
| 2014 |
| 2013 |
| 2014 |
| 1 |
| 2014 |
| 2013 |
| 1014 |
| 1 |
| 2014 |
对于④当0≤x＜1时，G（x）=x+[x]=x+0=x，当1≤x＜2，则G（x）=x-1，
当2≤x＜3，则G（x）=x-2，
当3≤x＜4，则G（x）=x-3
…
当-1≤x＜0，则0≤x+1＜1，则G（x）=G（x+1）=x+1，
当-2≤x＜-1，则-1≤x+1＜0，则G（x）=G（x+1）=x+2，
当-3≤x＜-2，则-2≤x+1＜-1，则G（x）=G（x+1）=x+3，…
令y=0，则G（x）=|sinx|，在同一个坐标系中，画出函数y=G（x）和
y=|sinx|的图象，显然有7个交点，故④正确．
故其中正确的命题的序号为①③④．
故答案为：①③④
点评：本题是新定义题，考查函数的性质及应用，考查函数的定义域、值域以及函数的周期性，运用图象相交的交点个数来确定函数的零点个数，对定义的准确理解是迅速解题的关键．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
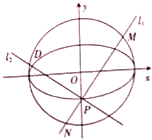已知椭圆E：