题目内容

对于正整数n，求证：1+
1
2
+
1
3
+…+
1
n
＞2（
n
-1）
考点：不等式的证明
专题：不等式
分析：不等式右边有个2，所以将不等式左边提取2变成：2(
1
2
+
1
2
2
+
1
2
3
+…+
1
2
n
)＞2(
1
2
+1
+
1
3
+
2
+
1
4
+
3
+…+
1
n
+
n-1
+
1
2
n
)=2(
2
-1+
3
-
2
+
4
-
3
+…
n
-
n-1
+
1
2
n
）=2(
n
-1)+
1
n
＞2(
n
-1)．
解答： 证明：1+
1
2
+
1
3
+…+
1
n
=2(
1
2
+
1
2
2
+
1
2
3
+…+
1
2
n
)＞2(
1
2
+1
+
1
3
+
2
+
1
4
+
3
+…+
1
n
+
n-1
+
1
2
n
)=2(
2
-1+
3
-
2
+
4
-
3
+…+
n
-
n-1
+
1
2
n
）=2(
n
-1)+
1
n
＞2(
n
-1)．
点评：考查放缩法证明不等式的方法，想着用放缩法的原因是：不等式右边是2(
n
-1)，所以不等式左边提取2，并想法消去中间项，这样便可以想着用放缩法．
练习册系列答案
相关题目
函数f（x）=（3-x）ex的单调递增区间是（　　）
A、（-∞，2）
B、（0，3）
C、（1，4）
D、（2，+∞）
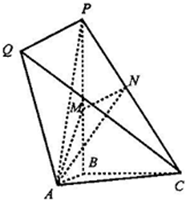如图所示的几何体中，PB⊥面ABC，PQ∥AB，PQ=PB=1；Rt△ABC中，∠ABC=90°，AB=BC=
1
2
．
（1）求QC与面ABC所成角的正弦值；
（2）过点A且与直线QC垂直的平面AMN与直线PB，PC分别交于点M，N，求线段MN的长度．
已知椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的离心率e=
3
2
，经过点（0，1）．
（Ⅰ）求该椭圆的方程；
（Ⅱ）设直线l与椭圆相交于不同的两点A、B，已知点A的坐标为（-a，0）．若|AB|=
4
2
5
，求直线l的方程．
有6名同学站成一排，求：
（1）甲不站排头也不站排尾有多少种不同的排法；
（2）甲不站排头，且乙不站排尾有多少种不同的排法；
（3）甲、乙、丙不相邻有多少种不同的排法．
已知z=1+i，如果z2+az+b=（1-i）（1-z），求实数a、b的值．
数列{an}的首项a1=1，前n项和Sn，n＞1时，3tSn-（2t+3）Sn-1=3t（t＞0）恒成立．    
（Ⅰ）求证：数列{an}是等比数列；
（Ⅱ）设数列{an}的公比为f（t），令b1=1，且n≥2时，bn=f（
1
bn-1
），求数列{bn}的通项公式；
（Ⅲ）求和：b1b2-b2b3+b3b4-…+b2n-1b2n-b2nb2n+1．
已知函数f（x）=Asin（ωx+φ），x∈R（其中A＞0，ω＞0，0＜φ＜
π
2
）的图象，两条相邻对称轴的距离为
π
2
，且图象上一个最高点的坐标为（
π
6
，2）．
（1）求函数f（x）的解析式；
（2）求函数f（x）的对称中心坐标和对称轴方程．
设a、b为实数，若复数
1+2i
a+bi
=1+i，则a=
 
，b=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网