题目内容
（Ⅰ）证明二维形式的柯西不等式：（a2+b2）（c2+d2）≥（ac+bd）2（a，b，c，d∈R）；
（Ⅱ）若实数x，y，z满足x2+y2+z2=3，求x+2y-2z的取值范围．
（Ⅱ）若实数x，y，z满足x2+y2+z2=3，求x+2y-2z的取值范围．
考点：二维形式的柯西不等式
专题：不等式的解法及应用
分析：（I）用作差比较法证明（a2+b2）（c2+d2）≥（ac+bd）2成立．
（II）利用柯西不等式求得 （x+2y-2z）2≤27，可得x+2y-2z的取值范围．
（II）利用柯西不等式求得 （x+2y-2z）2≤27，可得x+2y-2z的取值范围．
解答：
解：（I）证明：∵（a2+b2）（c2+d2）-（ac+bd）2 =a2d2-2adbc+b2c2=（ad-bc）2≥0，
∴（a2+b2）（c2+d2）≥（ac+bd）2成立，当且仅当ad=bc时取得等号．
（II）∵（x+2y-2z）2≤（x2+y2+z2）（12+22+（-2）2） 3×9=27，
∴-3
≤x+2y-3z≤3
．
∴（a2+b2）（c2+d2）≥（ac+bd）2成立，当且仅当ad=bc时取得等号．
（II）∵（x+2y-2z）2≤（x2+y2+z2）（12+22+（-2）2） 3×9=27，
∴-3
| 3 |
| 3 |
点评：本题主要考查用作差比较法证明不等式，柯西不等式的应用，属于基础题．
练习册系列答案
相关题目
已知x＞0，y＞0，且2x+y=1，则
+
的最小值为（ ）
| 1 |
| x |
| 1 |
| y |
| A、3 | ||
B、2+3
| ||
C、3+2
| ||
D、2-3
|
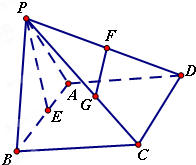如图，四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，△PAB是等边三角形，E、F、G分别是AB、PD、PC的中点．