题目内容
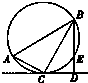如图，在△ABC中，∠ACB=90°，∠A=60°，AB=20，过C作△ABC的外接圆的切线CD，BD⊥CD，BD与外接圆交于点E，求DE的长．考点：与圆有关的比例线段
专题：立体几何
分析：由已知得∠ABC=30°，AC=10，BC=10，∠BCD=∠A=60°，BD=15，CD=5
，由切割线定理，得CD2=DE•DB，由此能求出DE．
| 3 |
解答：
解：∵在△ABC中，∠ACB=90°，∠A=60°，
∴∠ABC=30°，
∵AB=20，∴AC=10，BC=10
，
∵CD为切线，∴∠BCD=∠A=60°，
∵∠BDC=90°，∴BD=15，CD=5
，
由切割线定理，得：
CD2=DE•DB，即75=15DE，
解得DE=5．
∴∠ABC=30°，
∵AB=20，∴AC=10，BC=10
| 3 |
∵CD为切线，∴∠BCD=∠A=60°，
∵∠BDC=90°，∴BD=15，CD=5
| 3 |
由切割线定理，得：
CD2=DE•DB，即75=15DE，
解得DE=5．
点评：本题考查线段长的求法，是中档题，解题时要认真审题，注意切割线定理的合理运用．
练习册系列答案
名校课堂系列答案
相关题目
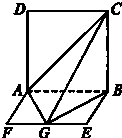如图所示，平面ABCD⊥平面ABEF，ABCD是正方形，ABEF是矩形，且AF=