题目内容
从区间[-5,5]内随机取出一个数x,从区间[-3,3]内随机取出一个数y,则使得|x|+|y|≤4的概率为 .
考点:几何概型
专题:计算题,概率与统计
分析:从区间[-5,5]内随机取出一个数x,从区间[-3,3]内随机取出一个数y,对应的区域是长方形,使得|x|+|y|≤4,落在矩形内的部分,分别求出面积,即可得出结论.
解答:
 解:从区间[-5,5]内随机取出一个数x,从区间[-3,3]内随机取出一个数y,对应的区域面积为60,
解:从区间[-5,5]内随机取出一个数x,从区间[-3,3]内随机取出一个数y,对应的区域面积为60,
使得|x|+|y|≤4,落在矩形内的部分,如图所示,面积为2×
×(2+8)×3=30,
∴所求概率为
=
.
故答案为:
.
 解:从区间[-5,5]内随机取出一个数x,从区间[-3,3]内随机取出一个数y,对应的区域面积为60,
解:从区间[-5,5]内随机取出一个数x,从区间[-3,3]内随机取出一个数y,对应的区域面积为60,使得|x|+|y|≤4,落在矩形内的部分,如图所示,面积为2×
| 1 |
| 2 |
∴所求概率为
| 30 |
| 60 |
| 1 |
| 2 |
故答案为:
| 1 |
| 2 |
点评:本题主要考查几何概型的概率公式的计算,确定区域的面积是解决本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知关于x的一元二次方程x2-(k-1)x+1=0有两个实根,则k的取值范围为( )
| A、[-1,3] |
| B、(-∞,-1]∪[3,+∞) |
| C、(-1,3) |
| D、(-∞,-1)∪(3,+∞) |
若函数f(x)=x2+mx+1有两个不同的零点,则实数m的取值范围是( )
| A、(-1,1) |
| B、(-2,2) |
| C、(-∞,-2)∪(2,+∞) |
| D、(-∞,-2)∪(1,+∞) |
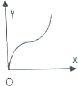
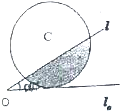 如图,已知直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是( )
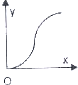
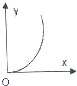
如图,已知直线l和圆C,当l从l0开始在平面上绕点O按逆时针方向匀速转动(转动角度不超过90°)时,它扫过的圆内阴影部分的面积y是时间x的函数,这个函数的图象大致是( )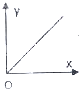
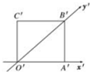 如图,正方形O′A′B′C′的边长为acm(a>0),它是一个水平放置的平面图形的直观图,则它的原图形OABC的周长是
如图,正方形O′A′B′C′的边长为acm(a>0),它是一个水平放置的平面图形的直观图,则它的原图形OABC的周长是 如图,已知边长为1的正方形ABCD位于第一象限,且顶点A、D分别在x,y的正半轴上(含原点)滑动,则
如图,已知边长为1的正方形ABCD位于第一象限,且顶点A、D分别在x,y的正半轴上(含原点)滑动,则